Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Hexy-metry
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
This very good solution came from The Maths Club at Wilson's School :
The interior angles of the hexagon are all equal to 120 degrees by symmetry.
Let O be the centre of the circle, with radius $r$. Considering triangle BCD, by the cosine rule,
$$BD^2 = a^2 + b^2 - 2ab \cos 120.$$
Considering triangle BOD, by the cosine rule,
$$BD^2 = 2r^2 - 2r^2 \cos 120.$$
As $ \cos 120 = -\frac {1}{2}$, we have $a^2 + b^2 + ab = 3r^2$ so
$$r = \sqrt {{a^2 + b^2 + ab\over 3}}.$$
 |
Ruth from the Manchester High School
for Girls proves the figure has rotational symmetry of order 3 and
the angles are 120 degrees as follows, and then goes on to find the
solution using the Cosine Rule as above:
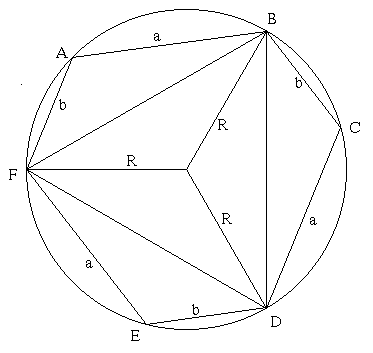
Let O be the centre of the circle and $R$ be the radius.
Construct the radii OA, OB, OC, OD, OE and OF. This creates 6
isoceles triangles, 3 with sides $R, R$ and $a$ and 3 with sides
$R, R$ and $b$, therefore by SSS congruence, angles
FAO=AFO=CBO=BCO=DEO=EDO and BAO=ABO=CDO=DCO=FEO=EFO therefore the
angles of the hexagon are all 120 degrees. ACE and FBD are therfore
equilateral triangles.
|
|
Matt, who did not reveal his school,
used a different method not involving the Cosine Rule.
This hexagon is formed by drawing an equilateral triangle over
a circle where the centre of the circle coincides with the centre
of the triangle and joining the points at which the triangle
crosses the circle. The shorter edge of the hexagon has length $FB=
a$ and the longer has length $b$. Therefore line AB has length
$\frac {a}{2}$ and line BD has length $b$.
Constructing the equilateral triangle BCD defines line BC as
having length $b$. So line AC has length $\frac{a}{2}+b$.
|
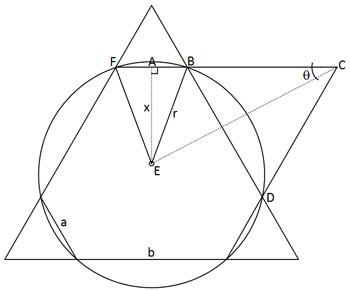 |
Let line AE have length $x$. The radius has length $r$. From
triangle ABE and using Pythagoras:
$$r^2 = x^2 +\left({\frac{a}{2}}\right)^2.$$
From triangle ACE: $$\tan \theta = \frac{x}{\frac{a}{2} +b}$$
but, $\theta = 30^o$ (since it is half the internal angle of an
equilateral triangle) so, $$x = \frac{1}{\sqrt 3}\left( \frac{a}{2}
+b \right).$$ Therefore, by eliminating $x$ between these
expressions and simplifying, we get:
$$r = \sqrt {{a^2 + b^2 + ab\over 3}}.$$