Copyright © University of Cambridge. All rights reserved.
'Ordered Sums' printed from https://nrich.maths.org/
Show menu
Let a(n) be the number of ways of expressing the integer n as an ordered sum of 1's and 2's. For example, a(4) = 5 because:
| 4 = | 2 + 2 |
| 2 + 1 + 1 | |
| 1 + 2 + 1 | |
| 1 + 1 + 2 | |
| 1 + 1 + 1 + 1. |
Let b(n) be the number of ways of expressing n as an ordered sum of integers greater than 1.
| (i) | Calculate a(n) and b(n) for
n 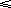 8. What do
you notice about these sequences? 8. What do
you notice about these sequences? |
| (ii) | Find a relation between a(p) and b(q). |
| (iii) | Prove your conjectures. |