Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Ordered Sums
Age 14 to 16
Challenge Level 





- Problem
- Student Solutions
Let a(n) be the number of ways of expressing the integer n as an ordered sum of 1's and 2's. For example, a(4) = 5 because:
| 4 = | 2 + 2 |
| 2 + 1 + 1 | |
| 1 + 2 + 1 | |
| 1 + 1 + 2 | |
| 1 + 1 + 1 + 1. |
Let b(n) be the number of ways of expressing n as an ordered sum of integers greater than 1.
| (i) | Calculate a(n) and b(n) for
n 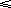 8. What do
you notice about these sequences? 8. What do
you notice about these sequences? |
| (ii) | Find a relation between a(p) and b(q). |
| (iii) | Prove your conjectures. |