Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
A Shade Crossed
Age 14 to 16
Challenge Level 





- Problem
- Student Solutions
There were two solutions from Madras College, one from Thomas, James, Mike and Euan and the other from Sue Liu which is reproduced below.
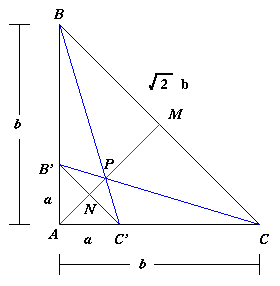 |
This triangle is a right angled isosceles triangle, the
hypotenuse being $\sqrt{2}b$. We draw a line through $A$ and point
$M$, the midpoint of the line $BC$. We draw the line $B`C`$ giving
another right angles isosceles triangle $AB`C`$, similar to
triangle $ABC$ but with sides a and hypotenuse $\sqrt{2}a$. Now $N$
is the point where the line $B`C`$ meets the line $AM$, and $P$ is
the point where $BC`$ meets $B`C$ (also on $AM$).
It is clear that triangle $PBC$ is similar to triangle $P
B`C`$ and the enlargement factor from $B`C`$ to $BC$ is $b/a$. So
the line $PM$ is $b/a$ times as long as the line $PN$. Also the
line $AN$ is half the length of $B`C`$, so it is $\sqrt{2}a/2$. The
line $AM$ is half the length of $BC$ so it is $\sqrt{2}b/2$.
|
If we let $PN$ be $x$ then we have an equation:
$$x + \frac{bx}{a} + \frac{\sqrt{2}}{2}a =
\frac{\sqrt{2}}{2}b$$
Solving this equation gives $$x =
{\frac{\sqrt{2}}{2}}{\frac{(b - a)a}{(a + b)}}$$
$PM$ is the height of the shaded triangle and $PM =
xb/a$.
Area of the shaded triangle is:
$$\frac{xb}{a} \cdot \frac{\sqrt{2}}{2} \cdot b =
\frac{b^{2}(b - a)}{2(b + a)}$$