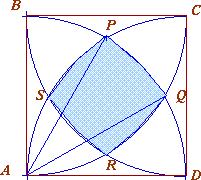$AD = 1$ unit, which is the radius of the circle centre $A$.

The coordinates of $P$ are $(AD \cos 60^{\circ} , AD \sin 60^{\circ} ) = ({1\over2}, {\sqrt{3}\over2})$

Similarly coordinates of $Q$ are $(AD \cos 30^{\circ} , AD \sin 30^{\circ} ) = ( {\sqrt{3}\over2},{1\over2})$ and angle $PAQ$ is $30^{\circ}$.

Area of square $PQRS = ({1\over2} - {\sqrt{3}\over2})^2 + ({\sqrt{3}\over2} - {1\over2})^2 = 2 - \sqrt{3}$

Area of a segment $PQ$ = [${1\over12}$ area of circle, centre $A$ radius $1$ unit] - [Area of Triangle $APQ$ ]

Using the formula ${1\over12}\pi r^2$ for the $30$ degree sector and ${1\over2} ab\sin C$ for the area of the triangle we get:

Area of a segment $PQ = {1\over12} \pi.1.1 - {1\over2}.1.1.{1\over2} = {\pi\over12} - {1\over4}$ \par Bounded area = area of square $PQRS$ + area of 4 equal segments

Bounded area $= 2 - \sqrt{3} + 4 ({\pi\over12} - {1\over4}) = 1 + {\pi\over3} - \sqrt{3}$