Bound to Be

'Bound to Be' printed from https://nrich.maths.org/

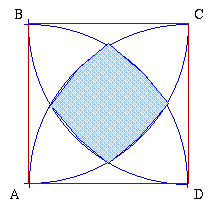$ABCD$ is a square of side 1 unit. Arc of circles with centres at $A, B, C, D$ are drawn in.

Prove that the area of the central region bounded by the four arcs is:

$(1 + \pi/3 + \sqrt{3})$ square units.