Giant Holly Leaf

Find the perimeter and area of a holly leaf that will not lie flat (it has negative curvature with 'circles' having circumference greater than 2πr).

Given a square ABCD of sides 10 cm, and using the corners as centres, construct four quadrants with radius 10 cm each inside the square. The four arcs intersect at P, Q, R and S. Find the area enclosed by PQRS.

Get Cross

A white cross is placed symmetrically in a red disc with the central square of side length sqrt 2 and the arms of the cross of length 1 unit. What is the area of the disc still showing?

Bound to Be

Age 14 to 16 Challenge Level:

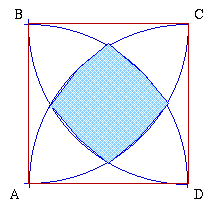$ABCD$ is a square of side 1 unit. Arc of circles with centres at $A, B, C, D$ are drawn in.

Prove that the area of the central region bounded by the four arcs is:

$(1 + \pi/3 + \sqrt{3})$ square units.

Pi. Arithmetic, Geometric and Harmonic Means. Circumference and arc length. Symmetry. Area - circles, sectors and segments. 2D shapes and their properties. Regular polygons and circles. Selecting and using information. Inequalities. Limits of Sequences.

You may also like

Giant Holly Leaf

Quadarc

Get Cross

Bound to Be

Age 14 to 16 Challenge Level: