Copyright © University of Cambridge. All rights reserved.
'Buzzy Bee' printed from https://nrich.maths.org/
Show menu
Why do this problem?
This problem gives children the chance to identify and continue number patterns, counting on and back in ones and twos. It is also a good chance for learners to understand the benefits of a trial and improvement approach.
Possible approach
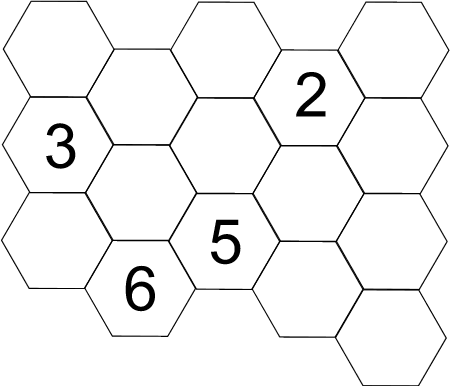
Before introducing the problem, you could do some counting outloud in ones and twos with the children. Go both forwards and backwards, and start from different numbers, not just 1 or 20. You could then have the honeycomb image displayed on an interactive whiteboard so that you and the class can annotate it as the lesson proceeds.
Begin by asking children to talk in pairs about where they think they could put another number. Invite one pair to write their suggestion on the honeycomb picture and ask them to explain why they decided on that number in that particular position. In this first instance, it may not be the 'correct' number, but there may be a good reason and it might be that the class will only realise it
doesn't work when there are more numbers on the honeycomb. This doesn't matter and is an important thing for children to appreciate - that trial and improvement is a good way of working on a problem, as we can learn from something which we find is wrong. Continue to build up a pattern on the board altogether until you feel the children understand the task, then leave them to work in pairs. They
will find it useful to have a print-out of the honeycomb picture.
When you come together again to share their solutions, focus on children explaining how they worked through the problem and why they chose certain numbers to go in certain positions.
Key questions
What number could follow on from this?
What number could come before this?
What number could come between these two numbers?
Does that number fit with the pattern in this part of the honeycomb too?
Possible extension
Learners could continue the honeycomb pattern to the right or left, or you could give children a this sheet with an empty honeycomb and ask them to fill it with their own number pattern.
Possible support
You could always fill in a few more numbers on the honeycomb before asking children to complete it.