Copyright © University of Cambridge. All rights reserved.
'Golden Ratio' printed from https://nrich.maths.org/
Show menu
The 'divina proporzione' or golden ratio, represented by the Greek letter phi, is derived from the equation below where $a$ and $b$ are parts of a line.
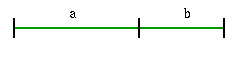 |
$a+b:a=a:b$
i.e. $ \frac{a+b}{a}=\frac{a}{b}=\Phi\ \quad $(phi)
|
If $b = 1$ show that
$\Phi = a = (\sqrt 5 + 1 )/2 = 1.618034...$.
In the following equation
what does $x$ equal?