One Big Triangle
Make one big triangle so the numbers that touch on the small triangles add to 10.
Problem
One Big Triangle printable sheet
Here are nine triangles. Each one has three numbers on it.
Your challenge is to arrange these triangles to make one big triangle, so the numbers that touch add up to 10.
Once you've finished making the big triangle, think about these questions:
How did you get started?
What did you do next?
You can print out the sheet at the top of this page and cut the triangles out, then try arranging them.
If you prefer, you can also use a printable version of the triangles with numbers represented on tens frames.
Alternatively, you might like to use this interactivity, which allows you to drag each triangle onto the large triangle.
Getting Started
You could try putting one piece in to start with and then seeing whether you can place another piece next to it.
The interactivity gives all the pieces in the correct orientation so you might like to use it to try out your ideas. If you would prefer to use cut-out pieces, you could check which way up each small triangle goes by looking at the interactivity.
Student Solutions
Shawn from Lanesborough School sent in this solution:
He added:
Step 1/ Put all the triangles in pairs to ten
Step 2/ Put all the red numbers together to make 10, do the same with blue and yellow
Step 3/ Make a hexagon, then the last three put them on with the coloured pairs.
Step 4/ Celebrate and write your maths down.
Ryan from Hayton Primary, Cumbria sent the same solution and wrote:
I started working from the top to the bottom with a small triangle.
I worked downwards to test out which was the right triangle to go at the top.
It took me about five tries to get the right triangle at the top.
When I got the right triangle at the top, all the other triangles were easy to fit in, working top to bottom.
Rowling Class from Manor School sent in the same picture and wrote:
Some of our class found it easy to start with but harder as you had to match two sides of the triangles at once. One group got stuck and had to start again with a different triangle.
It was really important to know your number bonds to 10. We used 10 - 7 to find out that we needed a triangle with a 3 to match with 7.
We were not surprised by the fact we found lots of different solutions.
Sophie managed to match one with colours as well as number bonds!
We also received our first solution from China in Chinese! Ma Xueying sent in this image which is the same solution as Shawn, Ryan and Rowling Class above:
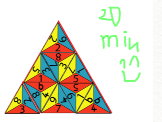
The translation of the Chinese shows a very interesting approach and can be found here.docx or here.pdf.
Cohen, Nate, Isla and Alex from Burke Ward Public School in Australia sent the following different solution:
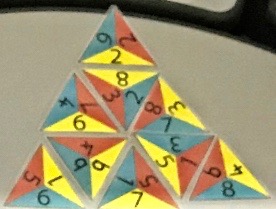We worked together and figured out how to make the numbers equal ten and make them into a triangle.
- we remembered our friends of 10
- we put the numbers together
- when it didn't make a triangle we pulled the triangles apart and started again.
When we finished we checked we had made a triangle and that the numbers equalled ten.
Cruz, Maddix, Lillah and Zak from Burke Ward Public School in Australia found the same solution and wrote:
We saw that they all make ten and it looks like a triangle. We didn't worry about the numbers, we focused on the triangle shape first. Then we sorted out the numbers by ten and making a triangle. We turned the little triangles around to make it. Sometimes we had to try again.
We knew when we were done because then we checked that we had a big triangle and the numbers touching were making their friends of ten.
Aidan, Alicia and Jimmie from Millfield Primary School found a third solution and said:
Aidan started at the top. I worked my way down until it made a big triangle. When you're making the triangle, if one piece has 8, you need to find another piece with a 2. Sometimes there are multiple pieces with 2 on them so I looked carefully at the other numbers on that piece to see which would fit best. I kept going until there were no pieces left. Jimmie helped to work out the number bonds using his fingers to make sure the number bonds were correct.
Alicia started at the bottom. I worked my way up and I found the right numbers for the number bonds. Sometimes I didn't have a piece that would fit, so I had to swap it with a piece already on the triangle.
Victoria, a teacher from Broadfield Academy in the United Kingdom, described her approach:
- First, I lined all the triangles in a long line playing with different combinations. I cut the line at various points to attempt to stack the triangle from bottom to top. Unsuccessful.
- Then, I looked for tiles with duplicate numbers and used those as a starting point in the middle of the triangle, then on the edge to exclude them from use. Unsuccessful.
- I noted which numbers appeared least frequently (e.g. 5). I used this starting point and moved tiles around the pair of fives. As it began to take shape the colour pattern confirmed I was on the right lines.
I found the solution after an hour of trial and error.
She felt it was great for revising number bonds to 10 and developing problem-solving and reasoning skills, and resilience!
Thank you all for sharing these different solutions. I wonder if there are more different solutions?
Teachers' Resources
One Big Triangle
One Big Triangle printable sheet
Here are nine triangles. Each one has three numbers on it.
Your challenge is to arrange these triangles to make one big triangle, so the numbers that touch add up to 10.
Once you've finished making the big triangle, think about these questions:
How did you get started?
What did you do next?
You can print out the sheet at the top of this page and cut the triangles out, then try arranging them.
If you prefer, you can also use a printable version of the triangles with numbers represented on tens frames.
Alternatively, you might like to use this interactivity, which allows you to drag each triangle onto the large triangle.
Why do this problem?
This problem is useful for consolidating number bonds to 10 and the corresponding subtraction facts. The novel context is likely to appeal to learners and encourage them to persevere. Children who are fluent with number bonds to 10 will still be challenged as the approach is not obvious, but logical reasoning will help them become more efficient in their search for a solution. The task will also draw on learners' geometrical reasoning too as they visualise triangles in different positions and orientations in order to solve the problem.
Possible approach
Using some already cut out pieces, or the interactivity on the screen, place a few triangles in the big triangle, making sure that touching faces add to 10. Invite children to gather round to see and ask them to think about what they notice. Again, take some contributions, and then introduce the task itself.
You could facilitate as many mini plenaries as you feel is helpful in order to share ideas that are being worked on around the room, including possible ways of getting started on the task. Learners' suggestions might include, for example, working top down, or bottom up, or hexagon out, matching colours, making pairs first, noticing the three 5s and therefore reasoning that one of these will have to be on an outer edge... If using the interactivity, they may realise that there are only three small triangles which are oriented so that they have a horizontal 'top' edge, so they may start with one of those to narrow down the possibilities.
Discuss the solutions that have been found. Are they all the same? If not, have they found all the possiblities?
Key questions
What do you need to put with ... to make 10?
Can you find a different card with that number on it?
What might be helpful to try next?
Possible extension
Children could be asked whether they can find more than one solution. How will they know whether another solution is the same or different to any they have already got? How will they know that they have found all the solutions?
Learners could also use the cards to make a shape (not necessarily a triangle) where the touching numbers add to 9 (or 8 or 11). Alternatively, they could add their own choice of numbers to blank triangular pieces to create their own activity.
Possible support
Children could use the cards to make a different shape (not necessarily a triangle) where the touching numbers add to 10, and/or the tens frame cards could be used to provide more support. Some children may find it difficult to cope with matching more than one pair of numbers at a time, in which case a domino activity would be more accessible. A set of nine-spot dominoes would be useful for this and you can find one on our printable resources page. The task could be to join the dominoes together so that the 'match' adds to 10 or any other number of the children's choice. This will then give them plenty of practice in identifying number bonds.