 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
X Is 5 Squares



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
A solution came from Tom of Lexden Primary School in Colchester, Essex. Tom explains how he set about solving the problem.
"I worked out what possibilities there were for multiplying the top two numbers together to equal the middle number. The two possibilities were 6 and 8 for the middle number.
I then worked out the other outside numbers so that when I added them altogether they would make 6 or 8. 8 didn't work."
So what did work? Tom knew, so did Ben and Thomas both pupils at Montgomery Church in Wales School, Powys.
They explain: "The middle number has to be 6 because that is the lowest number that is the one that four of the other lower numbers can total. That leaves 1, 2, 3 and 0 to be used around the outside. We multiplied pairs of these numbers together until we found one pair that made 6. These numbers were 2 and 3."
As Tom said, "The solution won't mirror image top to bottom because the top two numbers have to multiply to make the middle number."
Ben and Thomas agreed. They completed the task this way: "1 and 0 were then used to make the diagonal lines total the same amount."
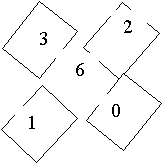
Emma and Francine found the same solution. They showed it the same way as Tom.
Well done to each of you. Are there any other series of consecutive numbers that will allow you to make a similar puzzle? Abigail who goes to Histon and Impington Infants School sent us in a very detailed solution to this problem. She wrote:
We named the squares with letters and then we wrote down the three rules in letters:
Well done! Thank you also to Katie, Kirsty, Sam, Lucija, Marek, Rosie, Sarah, Natasha, Nathaniel and William who told us they had each found one of the solutions.