Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Change Around
Age 5 to 7
Challenge Level 





- Problem
- Student Solutions
- Teachers' Resources
Change Around
Here is another triangular shape made from arranging circles.
Move just three of the circles so that the triangle faces in the opposite direction.
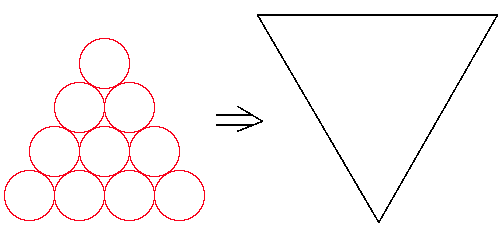
You could use this interactivity to try out your ideas:
Possible approach
This activity can be approached several ways in the classroom. Each child can be given a set of ten counters, coins or discs and asked to set up the triangle and then physically move the objects. A more abstract approach is to ask the children to draw the shape and visualise what changes can be made and then try them out. A third alternative is to use the interactivity provided and allow the children to move the red circles to form the new triangle.
It is an idea not to set the task with its condition of only three moves to begin with. Let the children explore the activity and then ask how many changes they had to make to reverse the direction of the triangle. Based on their input set the challenge: Can it be done in five or even four moves? How about just three moves? Before they start to solve for three moves invite the children to
think about, and then describe, which circles might be moved. As the task becomes more difficult the children are able to use what they have learned in the easier stages and visualise solutions to the more complex problem.
Key questions
Can you picture what the new triangle will look like?
Try moving some counters/balls and see what happens.
Can you do it in fewer moves?