 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
A Square Deal



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
A Square Deal
Complete the magic square using the numbers $1$ to $25$ once each.
Each row, column and diagonal adds up to $65$.
Each square is identified by its column and row:
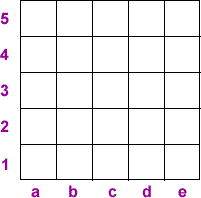
Here are the clues:
Perfect squares are in b5, b3, d3, b1 and c1.
Prime numbers are in a5, c5, e5, c4, a3, c3, e3, e2 and a1.
Triangular numbers are in d5, e4, d3, a1, e1 and c2.
Perfect cubes are in d3 and b2.
Powers of 2 are in b5, b2, e2 and b1.
Palindromic numbers are in a5 and d1.
Factors of 100 are in b5, d5, c4, b3, d3, a2 and e2.
The median of all the numbers is in c3.
Row 3 and column c are all odd.
Numbers that are the same upside-down are in a5, d3 and b2.
This problem is taken from the summer 2003 edition of "Mathematical Pie", a booklet of mathematical challenges published three times a year by The Mathematical Association. For more details about how to subscribe, see the MA website or phone 0116 221 0013.