You may also like

problem icon

Polydron

This activity investigates how you might make squares and pentominoes from Polydron.

problem icon

A Cartesian Puzzle

Find the missing coordinates which will form these eight quadrilaterals. These coordinates themselves will then form a shape with rotational and line symmetry.

problem icon

Hidden Meaning

What is the missing symbol? Can you decode this in a similar way?

Symmetry Challenge

Stage: 2 Challenge Level: Challenge Level:3 Challenge Level:3 Challenge Level:3

Christina from Marborough Primary, London has given this one some thought and made the sensible suggestion of trying to find all the symmetrical patterns with one coloured square, then with two squares, then three, then four. That's just what Tom has done below.

Tom was very careful to make sure he found them all. First, he looked for patterns with no coloured squares. Of course, there's only one of those:

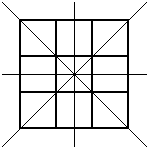
No shaded squares
Then he looked for patterns with one coloured square. He decided to count two patterns as the same if they were just rotations of each other, as otherwise there would be too many. Here are the patterns he found:
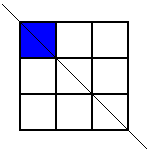
Top left square shadedTop centre square shadedCentre square shaded
Next he looked for patterns with two coloured squares. He had to be a bit more careful here, to make sure that he didn't miss any. First of all, he coloured in the top left square. Then he wondered whether he could find any patterns with this square coloured where the line of symmetry was vertical. He found this one:

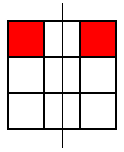
Top left and top right squares shaded
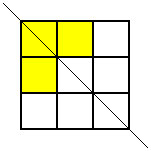
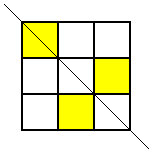
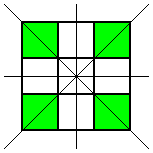
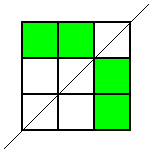
but that was the only one. Then he looked for patterns with this square coloured where the line of symmetry was horizontal, but he came up with the same one again (rotated, of course). Then he looked for ones where the line of symmetry was diagonal. Here are the two patterns he found:

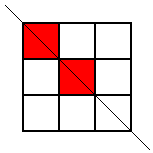
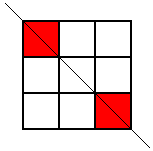
Top left and centre squares shadedTop left and bottom right squares shaded
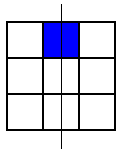
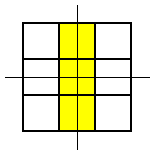
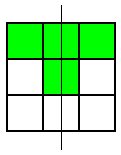
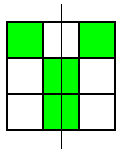
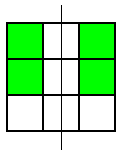
These were the only symmetrical patterns with a corner square shaded. Next he shaded the top centre square and looked for patterns with a vertical line of symmetry. Here's what he found:

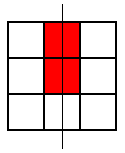
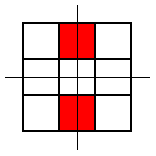
Centre top and centre squares shadedCentre top and centre bottom squares shaded
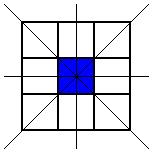
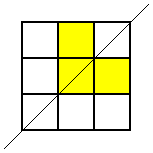
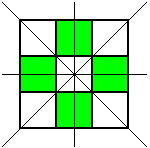
He noticed that he wouldn't get any new patterns by looking for ones with horizontal lines of symmetry, so he looked for patterns with a diagonal line of symmetry. This is the only one he found:
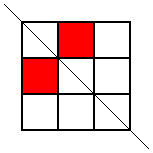
Middle left and top centre squares shaded
He used a similar system to find all the symmetrical patterns with three or four shaded squares. Here's what he found:
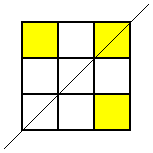
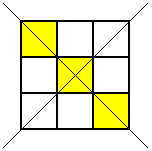
Top row shadedTop left, top right and centre squares shadedTop left, top right and bottom centre squares shadedTop left, top right and bottom right squares shadedTop left, centre and bottom right squares shadedTop left, top centre and middle left squares shadedTop left, middle right and bottom centre squares shadedTop centre, middle right and bottom centre squares shadedMiddle column shadedTop centre, centre and middle right squares shaded
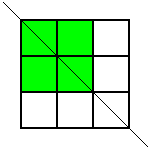
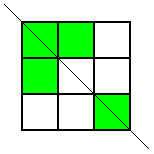
Top row and bottom centre square shadedTop row and bottom centre square shadedTop left, top right, centre and bottom centre squares shadedTop left, top right, middle left and middle right squares shaded Top left, top right, bottom left and bottom right squares shaded Top left, top centre, middle left and middle centre squares shaded Top left, top centre, middle left and bottom right squares shaded 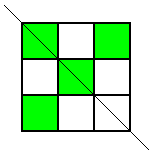Top left, top right, centre and bottom left squares shaded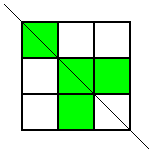Top left, centre, middle right and bottom centre squares shaded Top left, top centre, middle right and bottom right squares shaded Top centre, middle left, middle right and bottom centre squares shaded
Finally, Tom noticed that really these told him all of the symmetrical patterns, because he could imagine a coloured grid where the white squares were the ones that had been shaded, and these would give the patterns with five, six, seven, eight or nine shaded squares.
So Tom found 62 symmetrical patterns in all.
 
Children from Kellett School in Hong Kong, noticed that Tom had missed out one of the patterns.  Here is the image they sent:
 
 
 
So that makes a total of 64 possible solutions.  Well done!

The NRICH Project aims to enrich the mathematical experiences of all learners. To support this aim, members of the NRICH team work in a wide range of capacities, including providing professional development for teachers wishing to embed rich mathematical tasks into everyday classroom practice. More information on many of our other activities can be found here.
Copyright © 1997 - 2012. University of Cambridge. All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.