Homes

There are to be 6 homes built on a new development site. They could be semi-detached, detached or terraced houses. How many different combinations of these can you find?

Stairs

This challenge is to design different step arrangements, which must go along a distance of 6 on the steps and must end up at 6 high.

Let's Investigate Triangles

Vincent and Tara are making triangles with the class construction set. They have a pile of strips of different lengths. How many different triangles can they make?

Teddy Bear Line-up

Stage: 1 Challenge Level:

We received lots and lots of very well-described solutions to this Teddy Bear problem - I'm sorry that we can't mention everyone. It was interesting to see what you called a 'move'. Jessica decided that a move was a 'swap':

Four steps:
Start: BBBB RRRR YYYY GGGG
Step 1, Switch the second blue and the second red:
BRBB RBRR YYYY GGGG
Step 2, Switch the fourth blue and the fourth yellow:
BRBY RBRR YYYB GGGG
The fourth red is not used because that would result in two reds being side by side. Switching fourth with fourth makes it easier to keep track of what has been done.
Step 3, Switch the fourth red and the fourth green:
BRBY RBRG YYYB GGGR
Step 4, Switch the second yellow and the second green:
BRBY RBRG YGYB GYGR
The bears are now fully mixed-up. This is not a unique solution.

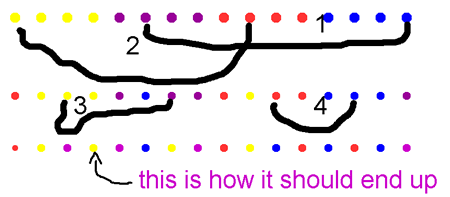
Jessica says this is not a unique solution, meaning that it can be done in four moves, but in different ways. Will, Milly and Emily from Swiss Gardens Primary School agreed with Jessica and sent in this picture of the four moves they made, which are slightly different from Jessica's:

Gemma and Maggie, also from Swiss Gardens, looked at simpler cases with smaller numbers of bears. They said:

We did $2\times2$ which was 1 move also $3\times3$ which was 2 moves.
$4\times4$ was 4 moves.

It can be useful to do this to see if you can identify and explain the pattern. I wonder whether you could predict the least number of moves for five lots of five bears?

Jodie thought about a 'move' in a different way and here is what she did:

If you call the blue bears B, the red bears R, the yellow bears Y, and the green bears G, you get:
B,B,B,B,R,R,R,R,Y,Y,Y,Y,G,G,G,G
1. Move one of the green bears to separate the first two blue bears:
B,G,B,B,B,R,R,R,R,Y,Y,Y,Y,G,G,G
2. Move one of the yellow bears to separate the second two blue bears:
B,G,B,Y,B,B,R,R,R,R,Y,Y,Y,G,G,G
3. Move one of the red bears to separate the last two blue bears:
B,G,B,Y,B,R,B,R,R,R,Y,Y,Y,G,G,G
4. Move one of the green bears to separate the second two red bears:
B,G,B,Y,B,R,B,R,G,R,R,Y,Y,Y,G,G
5. Move one of the yellow bears to separate the final two red bears:
B,G,B,Y,B,R,B,R,G,R,Y,R,Y,Y,G,G
6. Move one of the green bears to separate the final two yellow bears:
B,G,B,Y,B,R,B,R,G,R,Y,R,Y,G,Y,G

Elijah also used this idea and, like Gemma and Maggie, he investigated simpler cases. He even tried five lots of five bears as well:

I found that the smallest number of moves to mix up the four lots of four colours was $6$.

Call the bears a1, a2, a3, a4, b1, b2, b3, b4, c1, c2, c3, c4, d1, d2, d3, d4 (the letters mean different colours).

Move a1 between b1 and b2

Move a2 between b2 and b3

Move a3 between b3 and b4

Now you have a4, b1, a1, b2, a2, b3, a3, b4

You can't do it in less than 3 moves because in 4 bears coloured 'b' there are 3 pairs that need to be split up.

Now do the same for the c's and d's.

That is $6$ moves.

You can do other moves and get a different mixture at the end.

I tried it for two lots of two colours and could do that in $1$ move.

Then I tried it for three lots of three colours. This was a bit harder because it doesn't split into two halves and you have to mix the colours up. I did it like this:

Start with a1, a2, a3, b1, b2, b3, c1, c2, c3

Move a1 between b1 and b2

Move c1 between b2 and b3

Move a2 between c2 and c3

Now you have a3, b1, a1, b2, c1, b3, c2, a2, c3

I noticed that the sequence $1, 3, 6 ... $ is the start of the triangle numbers.

So then I thought that for five lots of five colours the answer would be $10$. I think this is right - I couldn't do it in less than $10$ moves.

I think these are right for the smallest numbers of moves because you can imagine the bears as pairs of two colours (like the two lots of two colours problem) and see how many moves it must take to mix them up.

Fantastic reasoning, Elijah, thank you for your detailed solution. We can really understand how you were thinking.

We also received the following message from a mum which I couldn't resist including!

My daughter was trying this as we came back from Science Festival today when her little brother found the solution: he picked all the sets of buttons she was using (for counters) and threw them in the air ... as they fell they all scattered ..."Mum! It's just ONE move when HE does it!" Not sure this is what you intended, though...

Compare bears. Combinations. Interactivities. Practical Activity. Tangram. Addition & subtraction. Investigations. Visualising. Working systematically. Counters.

You may also like

Homes

Stairs

Let's Investigate Triangles

Teddy Bear Line-up

Stage: 1 Challenge Level: