 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Semi-detached



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Correct solutions were recieved from Aashay of Farmington High,USA, Mary of Birchwood High School, Sana, Jenny, Chris and Rosion of Madras College, St. Andrews, Andrei of School 205 Bucharest and Chen of the Chinese High School, Singapore.
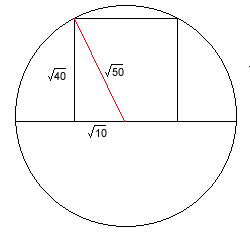
If a square has an area of $40$ sq units then its side is of length $ \sqrt{40} = 2 \times \sqrt{10}$.
Half the side is $ \sqrt{10}$.
So radius of the circle is $\sqrt{50} $.
Applying this to the square circumscribed by the whole circle
(see below)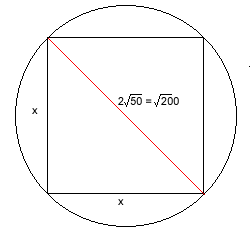
Diameter of the circle = diagonal of the square = $2 \times \sqrt 50 = \sqrt 200$
Let side of square $= x$ units. Area of the square = $ x^2$
Using Pythagoras' theorem:
$ x^2 + x^2 = 200 $
$ x^2 = 100 $
Therefore the area of the square is $100$ sq units.