 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Terminology



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Correct solutions from Mary of Birchwood High School and Andrei of School 205 Bucharest have contributed to the edited solution below.
As triangle DEF is equilateral, all its angles are $60$ .
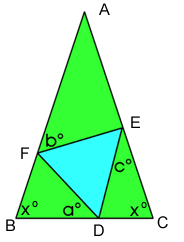
Angle AEF $= 180 - 60 - c = 120 - c$
Similarly
Angle BFD $= 120 - b$
Angle EDC $= 120 - a$
From triangle FAE, I calculate angle A:
As triangle ABC is an isosceles Angle ABC $=$ Angle ACB $= x$
Therefore $180 - (120 - b + a ) = 180 - (120 - a + c )$
Therefore $60 + b - a = 60 + a - c$
Therefore $2a = b + c$
Therefore $a = (b + c)/2$
Part Two
If $a=b=c$
Angle ABC $= 180 - (120 - b + a ) = 180 - (120 - a + a ) =
60$
Angle ACB $= 180 - (120 - a + c ) = 180 - (120 - a + a ) =
60$
Therefore angle BAC is $60$
Therefore triangle ABC is equilateral.