Copyright © University of Cambridge. All rights reserved.
'Reflecting Squarely' printed from https://nrich.maths.org/
Show menu
Reflecting Squarely printable sheet
Reflecting Squarely printable grids
The three pieces below can be fitted together to make shapes with at least one line of symmetry.
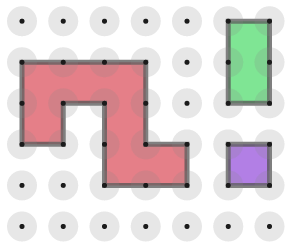
The vertices of each piece must lie on grid points, and you must not overlap two pieces.
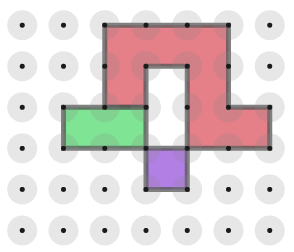
The pieces must be placed edge to edge, so this is not allowed.
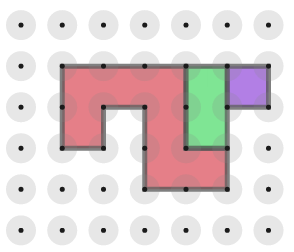
This arrangement does not satisfy the criteria because the shape does not have a line of symmetry.
Can you find all the possible solutions? (There are more than six.)
How can you be sure you've found them all?
Here are some further questions to explore:
Design your own set of three shapes, with a total area of 10 square units, as above.
How many ways can they be arranged to make symmetrical shapes?
Can you find a set of three such shapes which can be arranged into more symmetrical shapes than those in the original problem?
Can you find three such shapes which can never be arranged to make a symmetrical shape?
You may wish to print copies of the shapes.
Here is an interactive you might like to use to try out your ideas. The red dot can be used to rotate the pieces and the blue dot can be used to move the pieces. To flip the pink piece, click on it.
This problem is based on one found in the Dime "Line Symmetry A" pack, produced by Tarquin Publications
Click here for a poster of this problem.