Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Counting Binary Ops
Age 14 to 16
Challenge Level 





This question is about the number of ways of combining an ordered list of terms by repeating a single binary operation.
For example with three terms $a$, $b$ and $c$ there are just two ways $((a\oplus b)\oplus c)$ and $(a\oplus (b\oplus c))$. Suppose the binary operation $\oplus $ is just ordinary subtraction and $a=12, \; b=7, \; c=5$ then $((a\oplus b)\oplus c)= 5 - 5 =0$ and $(a\oplus (b\oplus c))= 12 - 2 = 10$.
We are not concerned in this question with doing the 'arithmetic' or with whether the answers are the same or different. We just want to find out how many ways there are of combining the terms, or if you like of putting brackets into the expression. Note that we need the brackets because the answers may be different as in the subtraction example.
These two tree diagrams show the two cases for combining 3 terms."
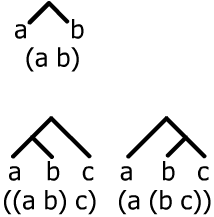
Show that for four terms, (three binary operations) there are five cases and find the number of cases for five terms and six terms.
See also the problems One Basket and Walkabout