Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Ruler
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
Andaleeb sent in this excellent solution.
The diagram shows some of the vertical lines drawn for values of x between 0 and 1 as described in the question. The lines are of height 1 unit at x = 0 and 1, of height ${1\over 2}$ units at $x= {1\over 2}$ , of height ${1\over 4}$ units at $x= {k\over 4}$ and ${1\over 8}$ units at $x= {k\over 8}$ and so on... up to ${1\over 2^5}$ at ${k\over 2^5}$ where $k$ is a positive integer.
| n | $0$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $\dots$ | $n$ | $n+1$ |
| Height | $1$ | ${1\over 2}$ | ${1\over 4 }$ | ${1\over 8}$ | ${1\over 16}$ | ${1\over 32 }$ | ${1\over 64}$ | $\dots$ | ${1\over 2^n}$ | ${1\over 2^{n+1`}}$ |
| Lines cut | $2$ | $1$ | $2$ | $4$ | $8$ | $16$ | $32$ |
$\dots$
|
$2^{n-1}$ | $ 2^n$ |
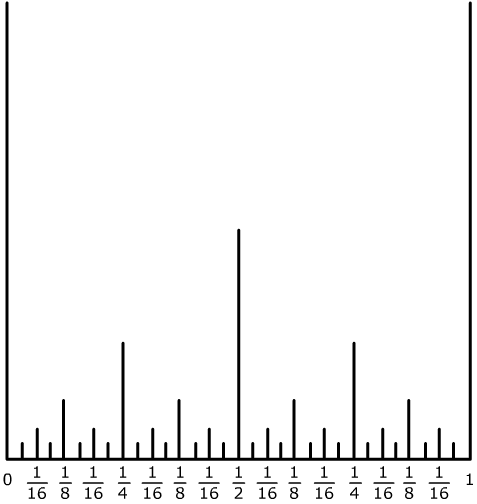
Thus if the height $h$ lies in ${1\over 2^n} > h> {1\over 2^{n+1}}$ then the number of lines cut is given by $$ 2 + 1 + 2 + 4 + 8 + ... + 2^{n-1} = 2 + {{2^n - 1} \over {2 - 1}} = 2^n + 1.$$ As $n$ tends to infinity the height of the lines tends to 0 and the number of lines cut tends to infinity.