Small Steps
Age 16 to 18
Challenge Level 
In both parts of this question we consider the limiting case of a process which is repeated infinitely often and things are not what they might seem to be.
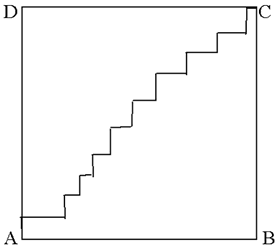
(a) In a square $ABCD$ with sides of length 1 unit a path is drawn from $A$ to the opposite corner $C$ so that the steps in the path are all parallel to $AB$ or parallel to $BC$ and not necessarily equal steps. Draw paths of this sort with 5 steps, 10 steps, 20 steps ... Find the total length of the path in each case. What would the length of such a path be if it had 1000 steps? What about the length of the path with 1 million steps? Is there anything surprising about this result? Suppose you keep increasing the number of steps in paths from $A$ to $C$ of this sort, putting in more and more and more steps. What can you say about the total length of the path?
(b) Now draw the graphs of $y={1\over 2^n}\sin 2^nx$ for $n= 1,2,3, ...$ and $0\leq x \leq 2\pi$. As $n$ tends to infinity the graphs oscillate more and more and get closer and closer to the $x$ axis. Prove that the length of the curve from $x=0$ to $x=2 \pi$ is the same for all values of $n$.
(a) In a square $ABCD$ with sides of length 1 unit a path is drawn from $A$ to the opposite corner $C$ so that the steps in the path are all parallel to $AB$ or parallel to $BC$ and not necessarily equal steps. Draw paths of this sort with 5 steps, 10 steps, 20 steps ... Find the total length of the path in each case. What would the length of such a path be if it had 1000 steps? What about the length of the path with 1 million steps? Is there anything surprising about this result? Suppose you keep increasing the number of steps in paths from $A$ to $C$ of this sort, putting in more and more and more steps. What can you say about the total length of the path?
(b) Now draw the graphs of $y={1\over 2^n}\sin 2^nx$ for $n= 1,2,3, ...$ and $0\leq x \leq 2\pi$. As $n$ tends to infinity the graphs oscillate more and more and get closer and closer to the $x$ axis. Prove that the length of the curve from $x=0$ to $x=2 \pi$ is the same for all values of $n$.
You may also like
Climbing Powers
$2\wedge 3\wedge 4$ could be $(2^3)^4$ or $2^{(3^4)}$. Does it make any difference? For both definitions, which is bigger: $r\wedge r\wedge r\wedge r\dots$ where the powers of $r$ go on for ever, or $(r^r)^r$, where $r$ is $\sqrt{2}$?
Little and Large
A point moves around inside a rectangle. What are the least and the greatest values of the sum of the squares of the distances from the vertices?
Approximating Pi
By inscribing a circle in a square and then a square in a circle find an approximation to pi. By using a hexagon, can you improve on the approximation?