Dodecawhat

1. The angles of a regular pentagon must all be 108°.
a) First I looked at the possibility of working with A4 paper.

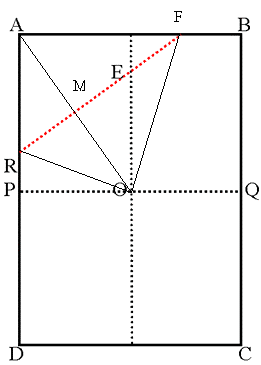
In the problem, I have to put A over O. So, triangles ARF and ORF are congruent, AM = MO and AO is perpendicular on FR.

As before, I note the smaller side of the paper (AB), with length x. Consequently, AD is $x\sqrt2$.

As P is on the middle of AD, AP = $x\sqrt2/2$. OP is x/2.

Triangle AOP is a right-angled triangle. As AP is parallel to EO, angles PAO and EOA are equal and, from the ratio of the side lengths of the paper, we get angle PAO = $tan^{-1}$ $(1\sqrt2)$ = 35.264 degrees.

As triangle MEO is also a right-angled triangle, angle EOM + angle MEO = $90^{\circ}$, so angle MEO is 54.736 degrees (to 3 decimal places).

But the figures (rectangle and then the pentagon) are symmetrical in respect to EO, so angle RES is two times angle MEO.

Angle RES = 2 $*$ MEO = $109.472^{\circ}$

The result is not $108^{\circ}$. The error is not so important, it is of the order of 1.4%

$${ {109.5^{\circ} - 108^{\circ}\over 108^{\circ}} = 1.4\%}$$

b) Now I have to calculate the new dimensions of the paper, so that I obtain a regular pentagon.

To make a regular pentagon in this way the ratio of the side lengths of the paper would have to be equal to tan 54⁰ , that is in the ratio 1.376 to 1 (to 4 significant figures) rather than 1.414 to 1 as in A4 paper.

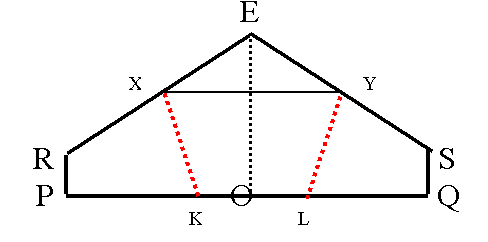
In the figure angle RES has a measure of 108°, XY is parallel to PQ and XK and YL are angle bisectors of angles RXY and SYX respectively.

Angles EXY and EYX are both equal to 36°. Consequently angles RXY and XYS both have a measure of 144°. Now, I calculate angle KXY:

KXY = RXY/2 = 72°

Now, I calculate angles EXK and EYL (the angles of the pentagon):

EXK = EYL = 72° + 36° = 108°

I observe that the other two remaining angles are also congruent (by symmetry), both having a measure of 108°.

So, I proved that in this case I obtain a regular pentagon.