We are going to make a pentagon. By making twelve such pentagons you can construct a dodecahedron like the one in the picture.

For each pentagon, you will need a piece of A4 paper and then follow the instructions below.

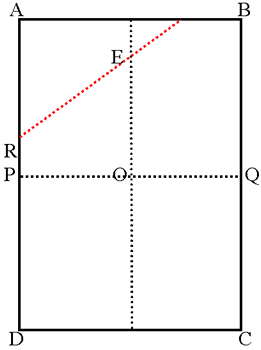Fold the paper in half both ways to find the centre O. Fold along the red line so A touches O. Fold C to O similarly. Fold B and D to O. Next fold along PQ. As the two halves come together,tuck the flap from corner D behind the flap from corner B to make 'pockets' (see the diagrams below).

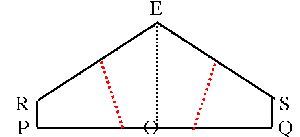Fold R and S up to the centre line EO, so that they meet to form a straight line and make a pentagon.

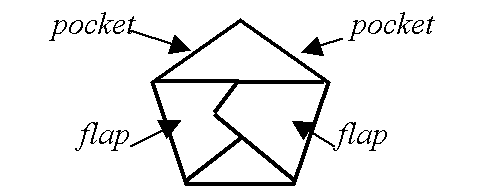
If you make 12 pentagons in this way and assemble them, using your 'flaps' and 'pockets', you can make a dodecahedron.

Now for the problem:

A4 paper has sides in the ratio$\sqrt2$ to $1$.

If you use A4 paper for this construction and try to make regular pentagons there is a small error in the angle at E. Find this error and find the dimensions of the paper which you would need to use to get an accurate regular pentagon and hence an accurate regular dodecahedron.

Below is another series of instructions to fold a pentagon from a sheet of A4 paper:

Fold corner C up to corner A.


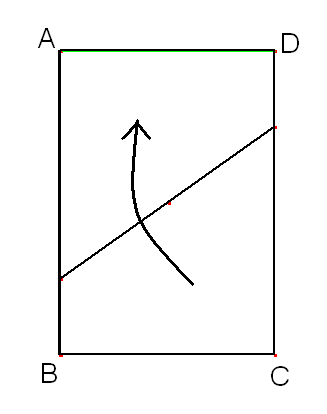
Your paper should now look like this:

  

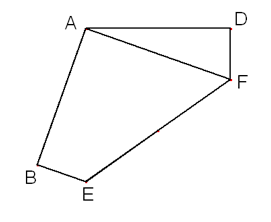
Now lay edge BE along edge DF to create a mirror line. Mark the crease for the mirror but do not fold:


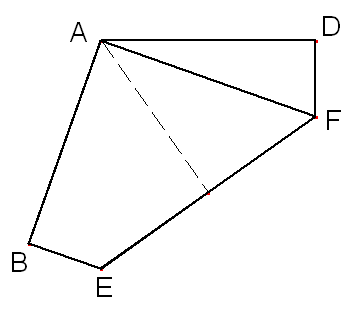
Lastly, fold edge BE to lie on the crease, then fold edge DF to lie on the crease.

If you do this you should get a pentagon like this:

 

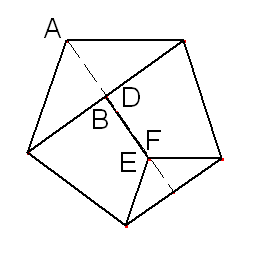
This pentagon might look quite different to the ones you made with the first series of folds, but the two shapes actually have the same angles!

Can you prove that the two different pentagons produced are similar?

How much smaller would my sheet of paper need to be to produce a pentagon the same size as my first ones?