Rots and Refs

Problem | Hint | Solution | Printable page |
Stage: 5 Challenge Level: Challenge Level:1

The point $P$ has coordinates $(r\cos \phi, r\sin \phi)$ where the distance of $P$ from the origin is $OP=r$ and the line $OP$ is at angle $\phi$ to the x axis. Find the image of this point under the transformation given by the matrix
\mathbf{T_1}=\left( \begin{array}{cc} cos \theta & -\sin \theta\\ sin \theta & cos \theta \end{array} \right)
Draw a diagram and describe the effect of this transformation on the points of the plane.

The point $P$ has coordinates $(p,q)$ and the point $P'$ is the reflection of $P$ in the line $y = x\tan\theta$. In the diagram below the lines $P'X'$ and $XA'$ are perpendicular to the line $OA'X'$. "

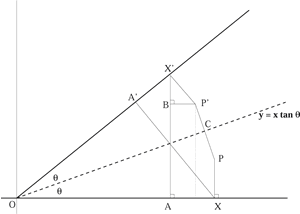
Reflection

Prove that $OX = OX' = p$, $P'X' = PX = q$ and $OA = OA' = p\cos 2\theta.$ Find the lengths $BP',\ AX'$ and $BX'$ and hence prove that transformation given by the matrix

\mathbf{T_2}=\left( \begin{array}{cc} cos 2\theta & sin2\theta\\ sin2\theta & -\cos2\theta \end{array} \right)
gives a reflection in the line $y=\tan\theta$.


search engine page

Published July 2003,August 2003.