Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Snookered
Age 14 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
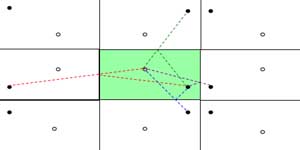
If you draw copies of the table reflected in the cushions then the reflection of the path of the ball after hitting a cushion appears as a straight line in the image of the table.
You may also like
Cushion Ball
The shortest path between any two points on a snooker table is the straight line between them but what if the ball must bounce off one wall, or 2 walls, or 3 walls?
Retracircles
Four circles all touch each other and a circumscribing circle. Find the ratios of the radii and prove that joining 3 centres gives a 3-4-5 triangle.
A Problem of Time
Consider a watch face which has identical hands and identical marks for the hours. It is opposite to a mirror. When is the time as read direct and in the mirror exactly the same between 6 and 7?