 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Some Spirals and Tessellations



 |
Aspiral is a curve formed by a point moving around a fixed point and constantly moving away from or approaching the fixed point. |
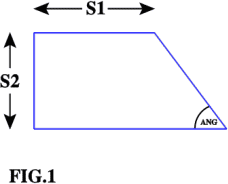
This month, building on the idea that many sets of things can be placed in a spiral configuration, we consider the following program based on Fig.1:
TO TRAP :S1 :S2 :ANG IF :S1 > 100 [STOP] FD :S1 RT :ANG FD :S2/SIN :ANG RT (180 - :ANG) FD :S1 + :S2 * TAN (90 - :ANG) RT 90 FD :S2 RT 90 FD :S1 LT (90 - :ANG) TRAP :S1/SIN :ANG :S2/SIN :ANG :ANG END
 |
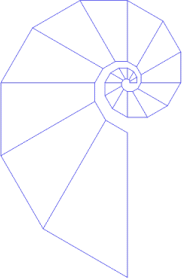 |
Try TRAP 5 25 60 as a starter for your investigations. See what spirals you can generate now.
While still in the realm of geometry a consideration of tessellations, tiles and tilings is long overdue.
Cundy C.M. and Rollett A. P. in 'Mathematical Models' give a good introduction to the plane tessallations.
First consider the three regular tessellations based on the square, equilateral triangle and regular hexagon respectively as below.
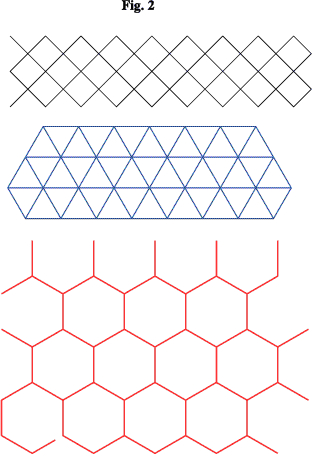
Can you devise a set of elegant procedures to illustrate these somewhat lacklustre tilings? But colour them much more imaginatively! [Hint: try drawing them freehand before thinking about construction procedures.]