Here is a recursive program

TO BRAN6 :T :A
IF 20 > :T [STOP]
FD :T RT :A
BRAN6 :T * (.6 + .02 * RANDOM 10) :A * (.7 + .04 * RANDOM 10) LT :A * 2
BRAN6 :T * (.6 + .02 * RANDOM 10) :A * (.7 + .04 * RANDOM 10) RT :A
BK :T
END

This produces a rather satisfying effect when the following is
tried:

HT BRAN6 220 25 BRAN6 220 45 BRAN6 220 55

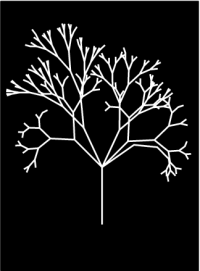
Why not experiment further by changing the values of variables :T and :A? Try if possible to anticipate what results before pressing the return key each time.

Why not experiment with greater/lesser degrees of randomness?

Any tentative conclusions?

Can you make smaller trees?
Smaller but stubbier trees?
Tall thin trees?
Tall and stubbier trees?

Any observations?

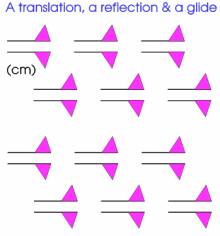
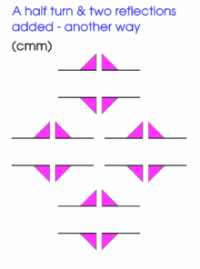
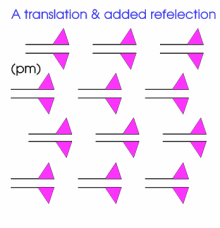
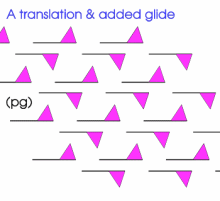
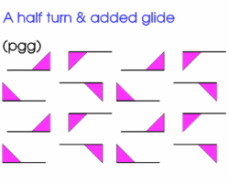
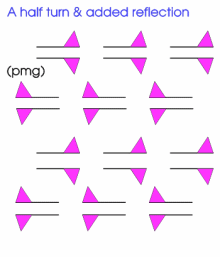
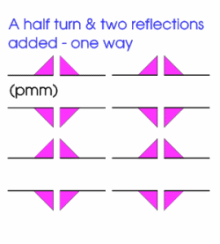
More geometrically, you might like to consider the following patterns.

They build on the patterns that went before, in that they are obtained from them by introducing a reflection or glide or both. There are 12 distinct patterns and each can be described according to an international system of coding.

The first seven are below. As before the invitation is for you to replicate these patterns (or with a much more flamboyant motif) using some elegant programming and to study these patterns yet further.