Below are two more recursive programs on a familiar theme that you might like to experiment with. Try varying the value of :T and or :A to see what effects you can achieve. Try if possible to anticipate what results when the variables are changed.

Why not experiment with greater degrees of randomness?

Can you make smaller trees? Smaller but stubbier trees? Tall thin trees?

TO BRAN5 :T :A
IF 30 > :T [STOP]
FD :T RT :A
BRAN5 :T * .7 :A * (.6 + .06 * RANDOM 10) LT :A * 2
BRAN5 :T * .7 :A * (.6 + .06 * RANDOM 10) RT :A
BK :T
END

Initially try BRAN5 250 45

TO BRAN6 :T :A
IF 20 > :T [STOP]
FD :T RT :A
BRAN6 :T * (.6 + .02 * RANDOM 10) :A * (.7 + .04 * RANDOM 10) LT :A * 2
BRAN6 :T * (.6 + .02 * RANDOM 10) :A * (.7 + .04 * RANDOM 10) RT :A
BK :T
END

Initially try BRAN6 230 35

Wallpaper patterns

Now, you might like to consider some patterns that can often be seen on wallpaper or fabrics or on car wheel trims. They are the five types of pattern involving the DIRECT ISOMETRIES. i.e those concerned with either a translation or rotation (of 60 °, 90 °, 120 ° and 180 °) of a motif.

We invite you to replicate these patterns (or to use more a flambouyant motif) with some elegant programming and to study these patterns yet further.
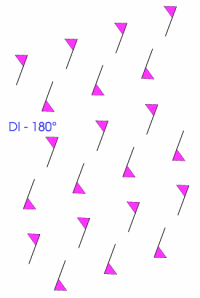
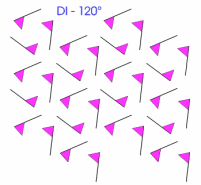
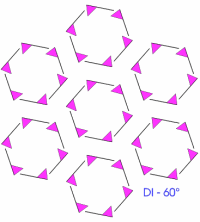
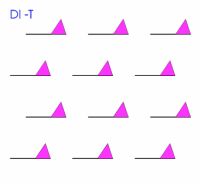