6 Beads

'6 Beads' printed from https://nrich.maths.org/

Show menu

6 Beads

If you put three beads onto a tens and ones abacus you can make the numbers 3, 30, 12 or 21.

The first abacus shows 0 tens and 3 ones; the second abacus shows 3 tens and 0 ones; the third abacus shows 1 ten and 2 ones; the fourth abacus shows 2 tens and 1 one.

Explore the numbers you can make using six beads.

Six loose beads are shown next to an empty abacus with spaces for tens and ones.

Can you find all the ways of using six beads?

How do you know you have found them all?

If you would like to try another task which involves finding all possible solutions, you could look at Three Ball Line Up.

Why do this problem?

This problem is a good, yet simple, activity that can get pupils thinking hard about numerals, numbers and place value. It also provides a context for discussing different ways of recording and for encouraging systematic working.

This task offers the chance to focus in particular on reasoning, problem solving and developing a positive attitude to mathematics, three of the five key ingredients that characterise successful mathematicians.

Possible approach

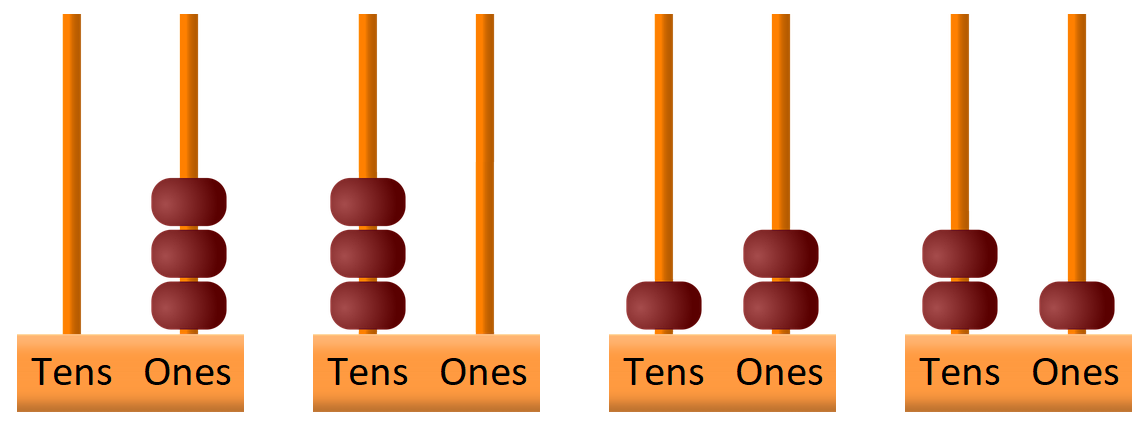
You could start the children off by showing them one of the examples for three beads and then asking for other ways the beads could be arranged, reading the numbers together. You may want to use a basic drawing of the abacus on an interactive whiteboard and have 'beads' to drag into place. At this stage, you could encourage learners to try and explain how we know we have all the different ways.

After this the children could work in pairs on the six beads problem so that they are able to talk through their ideas with a partner. Have available a range of equipment which they could use, but allow them to make their own choice. You may have, for example, a real abacus, counters, paper, beads, coloured pencils/pens etc. They could use digit cards to make the number which is represented on the abacus.

In a mini plenary, children could compare the ways in which they are beginning to record their findings and you could discuss the advantages of each. You could then talk about which recording methods might be best if we want to be sure that we had all the ways of using six beads. At this point, you could give them more time to work on the task, particularly enouraging them to consider how they will know that they have found all the solutions. You may find that some pairs change their recording method.

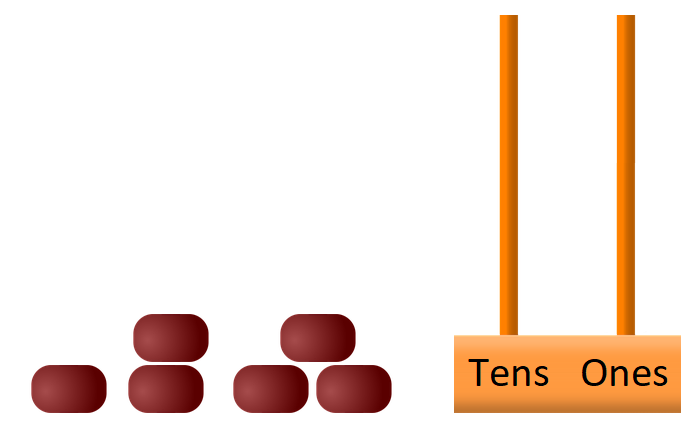
As you move around the room, ask some pairs to record one of their solutions on an abacus that you have pre-drawn. In the plenary, stick up those individual solutions on the board or wall and encourage the whole group to work together to make sure they have found all possibilities. Invite learners to reorder the solutions to reflect a pattern and use this to create any solutions that are not yet displayed. Emphasise that although they have worked together using one pattern, or one particular way of working systematically, there is no 'right' way to work systematically. There will be many different systems in the room and that should be celebrated.

Key questions

What can you tell me about the numbers you've found?

Are there any other ways you can arrange those beads?

How can you tell if you have them all?

Possible support

Some children may find it easier to use four beads, rather than going straight on to six. Using practical apparatus, such as counters, is essential for those having difficulties in understanding the problem. Learners could record individual solutions on individual pieces of paper, which could then be moved around and ordered to help them create a system.

Possible extension

Learners could increase the number of beads or they could be asked to investigate what would happen if there were three columns: units, tens and hundreds. If learners would like another context in which to practise working systematically, Three Ball Line Up would be an appropriate task.