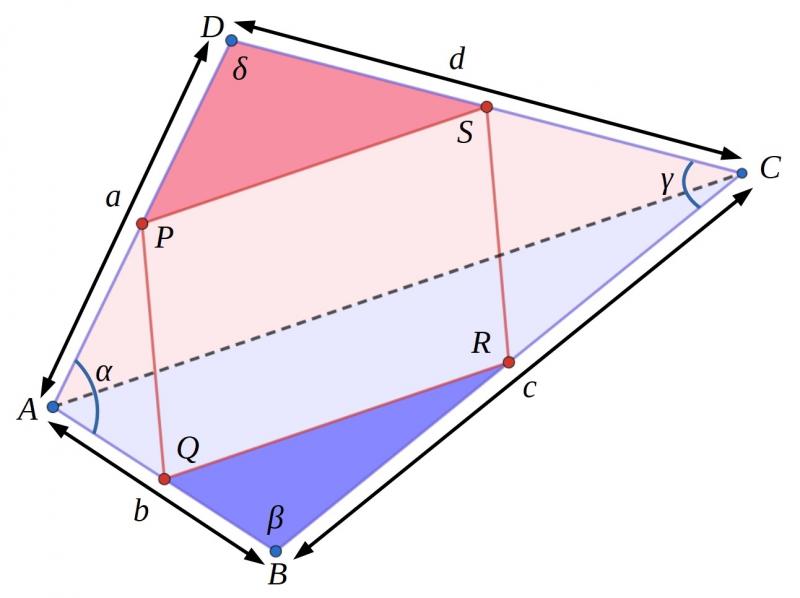
Quad in Quad - Area of PQRS proof
Can you rearrange the jumbled up statements to prove that the area of a quadrilateral is twice the area of the quadrilateral formed by joining its midpoints?
Age
14 to 18
Challenge level
Problem
In Quad in Quad you were asked to draw different convex quadrilaterals and then find the midpoints of the four edges.
You may have noticed that the quadrilaterals that were formed when joining the midpoints had half the area of the original quadrilaterals. But can you prove that this will always be the case?
Below is a diagram and a proof that has been scrambled up.
Can you rearrange it into its original order?
Image
