Minimal Connector
Problem
There are a variety of contexts in which it is important to be able to minimise the length of a network joining some fixed points, in order to minimise the use of resources or energy. This might be trying to create a gas pipeline connecting towns or creating a fibre-optic cable network.
Points on the network do not need to be connected directly to each other, but you must be able to get from any point to any other point on the network. The smaller the network is, the greater the environmental saving and the greater the efficiency of the system.
Imagine four points (they could be houses, or towns, or data points) arranged at the corners of a square of side length 10km.
Here are two possible ways to connect the four points:
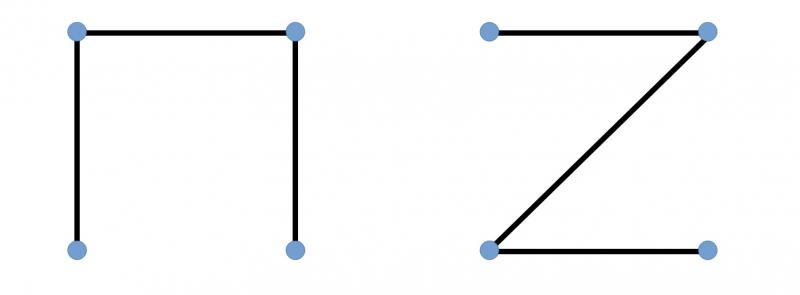
What is the total length of the network in each case? Can you find a better solution?
What is the minimum network that can connect them?
(A solution of less than 28km is possible!)
Alf, Charlie and Claire thought about this problem
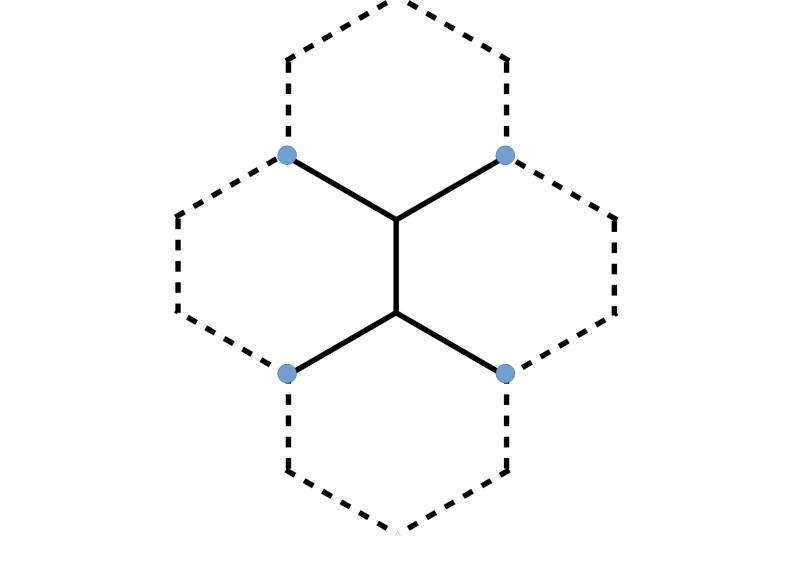
Charlie took inspiration from honeycombs to wonder if hexagons might be helpful. Click the button below to see what Charlie was thinking about. Can you use this to find a shorter path?
Claire remembered seeing bubbles made inside cubes, and thought that the minimum network might look similar. Click the button below to see what she thought the best solution might look like.
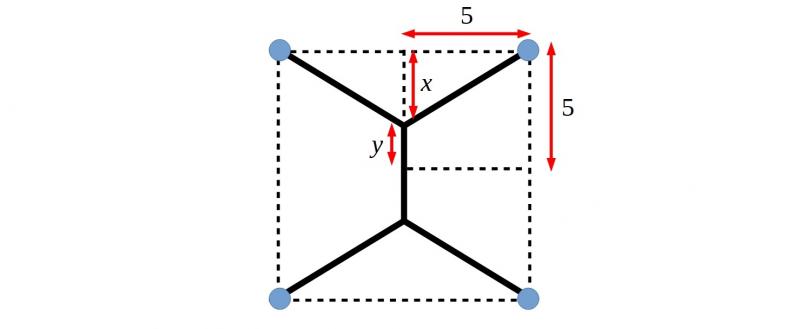
You can find out how to make bubbles inside cubes with this video from The Science Museum Group.
Both Alf and Claire used this idea to try and answer the question.
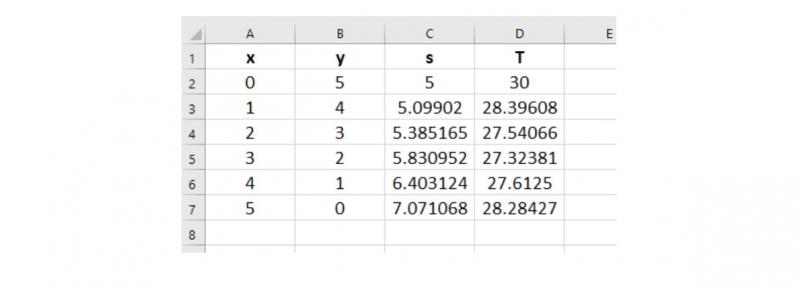
Alf thought that he might be able to use a spreadsheet to help him find a better solution. Click the button below to see his first spreadsheet. Can you use this idea to find the best solution?
Claire has learnt some Calculus techniques and thought she could use this to prove that she had the minimum length. If you have learnt some Calculus you might like to try to recreate her solution.
Then she differentiated this to find $\frac{\mathrm{d} L}{\mathrm {d} x}$, and used this to find the value of $x$ where this is equal to 0.
Then she used this value of $x$ to find the minimum value of $L$.
Finally she used Desmos to sketch a graph of $L$ to check her answer.
Do you get the same answer using all three approaches? Which approach do you prefer?
Once you have tried this problem, you might like to watch this video from James Grime where he uses bubble mixture to find the solution to this problem. He also shows how this can be adapted to other problems!
This problem is based on a problem from the book Teaching Mathematics as if the Planet Matters
Getting Started
You can find a network less than 30km long by using two straight lines.
The various approaches use these mathematical skills:
- Alf's method uses spreadsheets and a trial and improvement method, using Pythagoras to find the length of the slanting sides.
- Charlie's method uses right-angled trigonometry and angles of polygons.
- Claire's method uses differentiation (including the chain rule) to find the minimum value.
Student Solutions
Tommy from Homewood School and Sixth Form Centre in the UK found the total lengths of the first two networks and one shorter network:
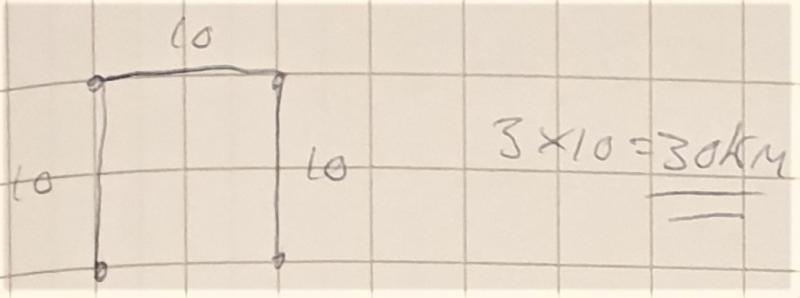
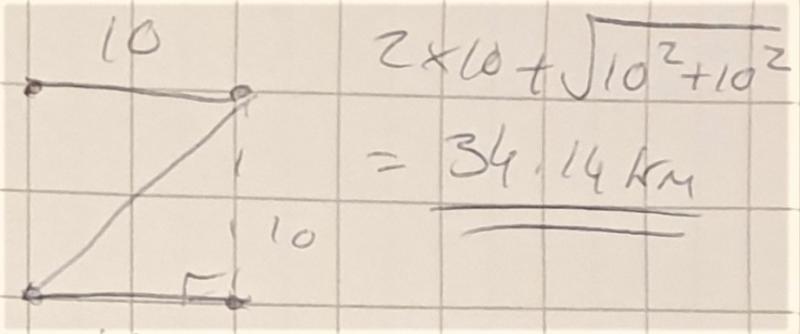

Lisa and students from Hollingworth in South Africa worked on finding the minimum network that could connect the 4 points. They wrote:
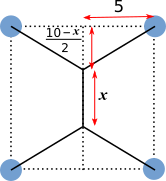
We created a method much like those of the the students, but did it before looking at them. We labeled our small bar in the middle $x$, then created this equation:
$y = 4\sqrt{\left(\frac{10-x}2\right)^2+25}+x$
Then graphed it in Desmos and found the minimum x to be 4.226, with the minimum total length (y) as 27.321
Tommy used calculus to find the minimum network (click here to see a larger version):

Teachers' Resources
This problem is suitable for both KS4 and KS5 students. It is based on a problem from the book Teaching Mathematics as if the Planet Matters
Alf's method uses spreadsheets and a trial and improvement method, using Pythagoras to find the length of the slanting sides.
Charlie's method uses right-angled trigonometry and angles of polygons.
Claire's method uses differentiation (including the chain rule) to find the minimum value.
Here is a video showing how a soap film can be used to find the minimal connector.
Here are some resources from the Royal Institution on the same problem.
This video from Matt Parker investigate minimal surfaces and has some nice bubble demonstrations in it!
This paper from Dr. Cyril Isenberg (MBE) explains how soap film can be used to solve problems. In this video Dr. Isenberg demonstrates some of the properties of bubbles.
This problem is one of a collection designed to develop students' carbon numeracy; we hope it will encourage students to think about the issues surrounding climate change. You can find the complete collection here.
This problem also featured in an NRICH Secondary webinar in November 2021.
