Age
11 to 16
| Article by
NRICH team
 | Published

Arclets explained



The Arclets problem set in September 2002 produced some very interesting and inspiring work from Madras College. This short article gives a flavour of the way that Sheila, Shona, Alison Colvin, Sarah, Kathryn and Gordan tackled the problem.

Each of the following shapes is made from arcs of a circle of radius r.

Arclets Explained

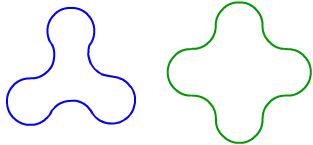
What is the perimeter of a shape with $3$, $4$, $5$ and $n$ "nodes".

What happens when $n$ is very large?

Explain the relationship between your answers and the perimeter of the original circle

Here are arclets with $3$, $4$ and $5$ nodes:

content-03-03-art1-3-pictures-here-1.gif
content-03-03-art1-3-pictures-here-2.gif
content-03-03-art1-3-pictures-here-3.gif

3-node solution

Arclets Explained
Arclets Explained

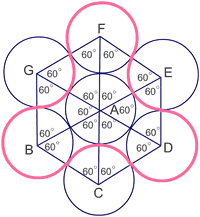
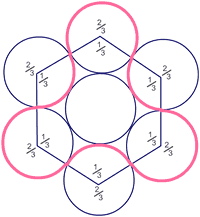
The angles at the centre of the inner circle are $60^{\circ}$

So the angles at the centre of the outer circles are $120^{\circ}$ and $240^{\circ}$ ($120^{\circ}+240^{\circ}= 360^{\circ}$.

We can therefore divide each circle into a $1/3$ ($120^{\circ}$ out of $360^{\circ}$) part and a $2/3$ ($240^{\circ}$ out of $360^{\circ}$) part.

The perimeter of the arclet is made up of 3 "inward" arcs of $1/3$ of the circumference and 3 "outward" arcs of $2/3$ of the circumference.

\begin{eqnarray} \mbox{Perimeter} &=&((3 \times \frac{1}{3}) + (3 \times \frac{2}{3}))\pi d \\ &= & (1 + 2)\pi d \\ &= & 3 \pi d \\ & = & 6 \pi r \end{eqnarray}

4-node solution

For the 4 node arclets the angles at the centre are $90^{\circ}$
Arclets Explained

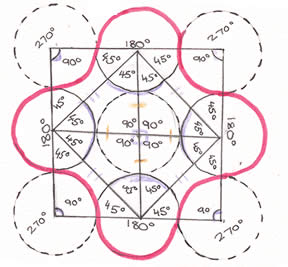
The inward arcs are $1/4$ of the circumference ($90^{\circ}$ - there are 4 inward arcs.

The outward arcs are $1/2$ of the circumference (4 lots of $45^{\circ}$ - there are 4 outward arcs.

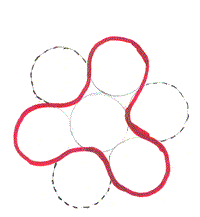
\begin{eqnarray} \mbox{Perimeter} &=&((4 \times \frac{1}{4}) + (4 \times \frac{2}{4}))\pi d \\ &= & (1 + 2)\pi d \\ &= & 3 \pi d \\ & = & 6 \pi r \end{eqnarray}

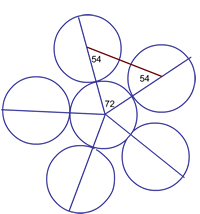
5-node solution

Because the inner circle is surrounded by five outer circles there are 5 angles - all of $72^{\circ}$ at the centre.

Using the properties of isoseles triangles the outward arcs are $2/5$ of the circumference and the inward arcs are $1/5$ of the circumference.



Arclets Explained
Arclets Explained
Arclets Explained
\begin{eqnarray} \mbox{Perimeter} &=&((5 \times \frac{1}{5}) + (5 \times \frac{2}{5}))\pi d \\ &= & (1 + 2)\pi d \\ &= & 3 \pi d \\ & = & 6 \pi r \end{eqnarray}

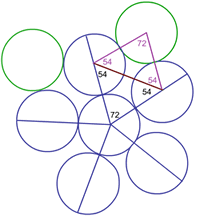
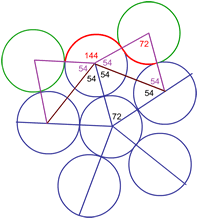
An image of part of the work Sarah, Kathryn and Gordon did to find the perimeter of the 5-node arclet is shown below

Arclets Explained

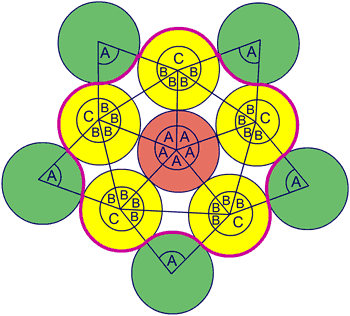
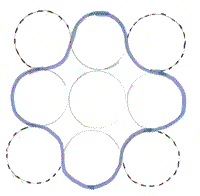
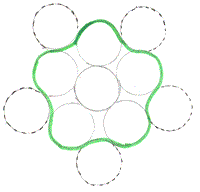
6-node solution

Scanned diagrams showing the work of Sheila, Shona and Alison to find the perimeter of a 6-node arclet:

Arclets Explained

 

\begin{eqnarray} \mbox{Perimeter for 6 nodes} &=&((6 \times \frac{1}{6}) + (6 \times \frac{2}{6}))\pi d \\ &= & (1 + 2)\pi d \\ &= & 3 \pi d \\ & = & 6 \pi r \end{eqnarray}

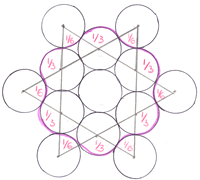
Finding the perimeter of the N - node arclet

We know that these are the equations for the perimeter of 3, 4, 5 and 6 node arclets:

Number of nodes

 3 4 5 6


Perimeter

$ \quad 3\times 2 \pi r = 6 \pi r \quad $


 $ \quad 3\times 2 \pi r = 6 \pi r \quad$ $ \quad 3\times 2 \pi r = 6 \pi r \quad $ $ \quad 3\times 2 \pi r = 6 \pi r \quad$

If we substitute $N$ for the node number we get (in every case):

\begin{eqnarray} \mbox{Perimeter for N nodes} &=&((N \times \frac {1}{N}) + (N \times \frac{2}{N}))\pi d \\ &= & (1 + 2)\pi d \\ &= & 3 \pi d \\ & = & 6 \pi r \end{eqnarray}


This is based on the fact that the angles at the centres of the circles will be $1/N$ of a full turn.

If $N$ is very large the node shape begins to look like a circle:

Arclets Explained

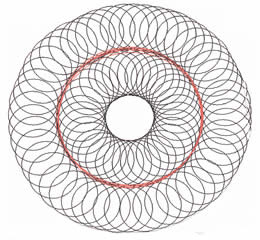
In other words. No matter how many nodes the perimeter will always be 3 circumferences.