Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Three Squares
Age 5 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Three Squares
What is the greatest number of squares you can make by overlapping three squares of the same size?
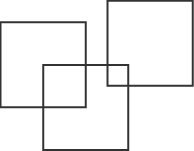
Please do send us pictures of the arrangements of your squares.
We would also like to know how you go about the task. How will you know if your way really does have the greatest possible number of squares?
You could use this interactivity to try out your ideas:
We would also like to know how you go about the task. How will you know if your way really does have the greatest possible number of squares?
You could use this interactivity to try out your ideas:
Why do this problem?
This problem is fantastic for reinforcing the properties of a square. The interactivity will enable learners to access the task immediately so they can easily begin to explore. This in turn means that they are much more likely to become curious about the challenge of finding as many squares as possible, so are motivated to work mathematically. The interactivity not only supports the exploratory nature of the problem, but also helps to deepen children's understanding of what makes a square a square.Possible approach
You could begin by using the interactivity to arrange just two squares in different ways and asking children to count the number of squares made in each case. It would be helpful if learners were invited to draw round each square they could see on the interactive whiteboard so that the squares were made easily visible. There might be some debate about which are squares and this gives the
group the opportunity to remind each other of a square's properties.
Once they are familiar with the idea, introduce the main problem and suggest they work in pairs. Ideally, children will be able to use the interactivity on a computer, laptop or tablet, but if not you could provide square frames cut from paper/card, or made using construction equipment/straws, or you could even print squares on three different transparent sheets for children to manipulate
themselves. It would also be useful to have squared paper available for jottings, rough working and recording.
In the plenary, you could use the interactivity to share solutions. It would also be worth talking about how children went about the problem. Did they record as they went along? If so, what and why? You may find that some learners drew an arrangement so that they could count the squares more easily by marking in colour. Others might have recorded an arrangement as a reminder of the largest
number of squares they had found so far.
Key questions
How many squares can you make by overlapping two large squares?
How do you know that is a square?
Can you move the large squares so that you create more squares?
How do you know that it isn't possible to make more squares?
How do you know that it isn't possible to make more squares?
Possible extension
Some children could try using four squares in the same way, or they could use equilateral triangles instead.