 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Five Coins



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Thank you to everybody who had a go at this activity. We received quite a variety of kinds of solutions to this problem with some children sending in one solution, some sending in a variety and some considering all the possibilities using 1p and 2p coins.
Jonathan sent in the following idea:
The answer could be for example £2.03.
Another solution was sent in by Lily:
I thought of a two pound and tried to make £2.01. So I times 50p by 4 which equaled £2.00.Then that meant I had one coin left which had to be 1p. So that only left adding them together. £2.00+1p= £2.01
Good ideas, both of you - you've noticed that we don't always use the largest value coins where we can, as we need Ben to have exactly five coins.
Faith from Ryde School with Upper Chine in England also worked out one possible total, and then went on to calculate the smallest and largest possible amounts:
He could have a 50p, 20p, 10p, 1p and 5p which makes 86p.
5 x 1p = 5p (Smallest)
5 x £2 = £10
Well done for working out the possible range of the amounts of money that Ben might have in his pocket - we only need to know the smallest and largest value coins in order to calculate this. We had similar solutions sent in from: Rachel; Dulcie; Erin, Charles, Cassius from Ryde School with Upper Chine in England; Dhruv from St Anne’s RC Primary in Manchester, UK; Amélie from St Nicholas CE Primary; Rosie from Red Hill; Dimitrios, Hollie, Betsy and Aaradhya from Pierrepont Gamston Primary School in the UK; and Ikjot from Westbrook Primary School in the UK.
Ryan from Garden International School in Malaysia also calculated the smallest and largest possible amounts, and began to think about the amounts that would be possible using only 1p and 2p coins:
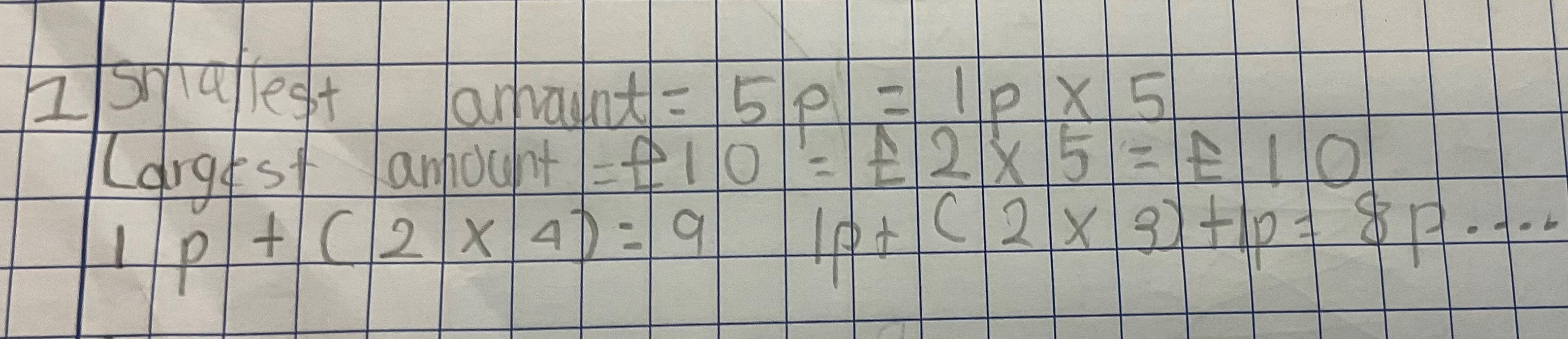
Can you see what the brackets mean in the last line of Ryan's working? What will come next after the '...'?
Dimitrios from Pierrepont Gamston Primary School in the UK showed how they calculated all the possibilities:
What if he still had five coins, but only 1ps and/or 2ps? How much might he have now?
1p 1p 1p 1p 1p= 5p
2p 1p 1p 1p 1p= 6p
2p 2p 1p 1p 1p= 7p
2p 2p 2p 1p 1p= 8p
2p 2p 2p 2p 1p= 9p
2p 2p 2p 2p 2p= 10p
This is a really systematic way of finding all the possible options! We also received similar solutions from: Faith from Ryde School with Upper Chine in England; Amélie from St Nicholas CE Primary; Rosie from Red Hill; and Hollie, Betsy and Aaradhya from Pierrepont Gamston Primary School in the UK. Thank you all for sharing your ideas with us.
We received a few solutions from children who considered this problem using dollars and cents rather than pounds and pence. Amrita said:
Minimum value 25c because 5c is the smallest value coin and maximum value is \$10 because \$2 is the highest value coin.
This is really interesting, Amrita - I can see how having a 5 cent coin as the smallest coin makes the smallest possible amount very different.
Kaleb from Covenant Christian Academy in the USA used pennies as well as 5 cent coins to think about what Ben might have in his pocket:
I used Pennies(P), Nickels(N), Dimes(D), Quarters(Q), and Dollar Coins(DC) to figure out this problem.
The smallest amount of money he could have is 5 cents. The largest amount of money he could have is 5 dollars. The amount of money he could have is as small as 5 cents or as large as 5 dollars.
If he still had five coins, but only pennies(p) and/or nickels(n)? He could have as small as 5 cents or as large as 25 cents. (Pennies have a value of 1 cent and nickels have a value of 5 cents.) The list of possibilities is:
5p, 4p+1n, 3p+2n, 2p+3n, 1p+4n, 5n
Have a look at these five possibilities - how many cents would Ben have in each case? Can you explain any patterns that you notice in these numbers?
Kaleb also sent in a picture where they began to work out all the possible amounts of money that Ben could have. Take a look at Kaleb's picture. How much money would each possibility add up to? Can you see any possibilities that Kaleb hasn't included?
If you're interested in exploring all the possible amounts of money Ben might have, take a look at our Five More Coins activity.
You may also like
Let's Investigate Triangles
Vincent and Tara are making triangles with the class construction set. They have a pile of strips of different lengths. How many different triangles can they make?