 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Published 2001 Revised 2019
Mouhefanggai
The material for this article was originally developed by Pat Perkins and presented in a talk by her daughter Sarah Perkins. The author is grateful to the family for giving permission to write this article.
This article derives the formula for the volume of a sphere, without using any mathematics more advanced than Pythagoras' theorem. It uses some ideas developed in the article Volume of a Pyramid and a Cone, which you may want to read first.
Volume of a mouhefanggai
Imagine two identical cylindrical pipes meeting at right angles. Now think about the shape of the space which belongs to both pipes. This is the shape that early Chinese mathematicians called the mouhefanggai. This can be translated as "two square umbrellas".


Making a mouhefanggai is tricky. You can slice two marrows so that they fit together like the pipes in the diagram. The bits you've sliced out can be put together to form a mouhefanggai. Alternatively, if you can find a couple of the square net umbrellas used to protect cakes from flies, this will make a reasonable approximation.
It might seem unlikely, but you can find a formula for the volume of a mouhefanggai using relatively elementary maths. This article will show you how to do this, and then go on to find the volume of a sphere, a formula which is often quoted but rarely proved without using calculus.
Observations about the mouhefanggai
Let's suppose that the cylinders have radius r, and that they are both lying on a horizontal plane. Then the mouhefanggai where they intersect has height $2r$. If we slice the mouhefanggai horizontally, each slice will be a square. The largest square, in the middle, will have sides length $2r$.
We can actually simplify things slightly, by dealing with just part of the mouhefanggai. We can cut it into eight identical pieces, by slicing it in three perpendicular directions. The horizontal cut gives a 'tent shaped' solid with a flat base and four curved 'walls'. This is cut into four with two perpendicular vertical cuts.
The difference solid
Take one of our pieces of the mouhefanggai, and imagine it fitting into a cube of side r, as shown:

Rather than finding the volume of the mouhefanggai piece, we shall actually find the volume of the rest of the cube; the difference-solid between the cube and the mouhefanggai piece.
Taking a slice


Now let's think again where that slice came from. If you look at this front view of the cube, you will see that $h$, $k$ and $r$ form a right-angled triangle. So using Pythagoras' Theorem, $r^2=h^2+k^2$. Rearranging this, we get $r^2-h^2=k^2$. So the area of the L-shape is $r^2-k^2=h^2$. Can you think of another solid, which when we take a slice at height $h$ gives us a slice of area $h^2$? In other words, the bottom slice has zero area, and the area gradually increases, to a top slice of area $r^2$.
When you have thought about this, you can look here for a picture of a solid which has slices with the same area as our difference-solid.
Well, we know how to find the volume of the shape on the left, and if all the slices are the same, the difference-solid must also have volume $\frac{r^3}{3}$.
Back to the mouhefanggai
If the cube has volume $r^3$ , and the difference-solid has volume $\frac{r^3}{3}$, then the mouhefanggai piece has volume $\frac{2}{3}r^3$. So the whole mouhefanggai has volume $\frac{16}{3}r^3$. Phew!
Comparing a sphere with a mouhefanggai
Although it surprised me that we could find the volume of a mouhefanggai like that, it's not a shape I can imagine needing to work with often. A sphere, though, is another matter. Most people have to just believe what they are told about the volume of a sphere until they have learnt calculus. But having found the volume of a mouhefanggai, it is a relatively small step to find the volume of a sphere.
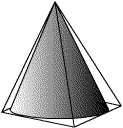
Think back to the previous article, where we found the volume of a cone by comparing it with the square-based pyramid it fitted into.
Now picture a sphere fitting snugly inside a mouhefanggai!
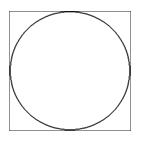
Any horizontal slice will consist of a circle radius $x$ inside a square of side $2x$. The area of the circle is $\pi x^2$. The area of the square is $2x \times2x=4x^2$. The ratio of the circle to the square is $\pi : 4$. So, for each slice, the area of the circle is $\frac{\pi}{4}$ the size of the area of the square. This means that the volume of the sphere will be $\frac{\pi}{4}$ the volume of the mouhefanggai. $\mbox{Volume of a sphere} = \frac{\pi}{4} \times\frac{16}{3}r^3= \frac{4}{3}\pi r^3$.
One to try yourself: doughnut
Imagine a perfect doughnut, and compare it to a cylinder:
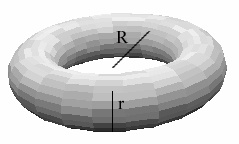
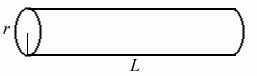
Slices at height x will look like this:

Compare the slices, and hence compare the volumes of the two solids.