 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Published 2001 Revised 2008
Incircles Explained
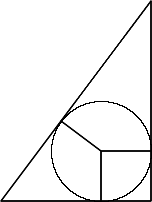
The largest circle which fits inside a triangle just touching the three sides of the triangle is called the inscribed circle or incircle. This article is about triangles in which the lengths of the sides and the radii of the inscribed circles are all whole numbers. Following on from the problem Incircles (February 2000) about right angled triangles we now find similar results for isosceles triangles.
Before you read on, can you find the radius of the inscribed circle of the triangle with sides of lengths 3, 4 and 5 units and then find the radius of the inscribed circle of the triangle with sides of lengths 5, 12 and 13 units? These numbers are Pythagorean triples, the triangles are right angled, the inscribed circle of the first has radius 1 unit and the second has radius 2 units. So can we find a right angled triangle with incircle of radius 3 units (or any other whole number) whose sides are a primitive Pythagorean triple? You'll find the answer to this question here .
The solution to the 'Incircles' problem shows that, for any circle whose radius is a whole number k, we are guaranteed at least one right angled triangle containing this circle as its inscribed circle where the lengths of the sides of the triangle are the a primitive Pythagorean triple:
It is certainly possible to construct triangles with sides a, b and c which give integer value to the incircle radius, but which are not a Pythagorean triple. One such is the isosceles triangle with sides 10, 10 and 12.
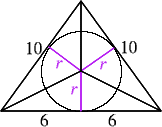
It is formed by putting two triangles back to back whose sides are given by the Pythagorean triple 6, 8, 10. As in the solution to the original problem, the radius r of the incircle is found by splitting the triangle into three and finding its area
$$\Delta = ({1\over 2}ar +{1\over 2}br +{1\over 2}cr)$$. HenceAnother such triangle is the 39, 39, 30 triangle which is formed from two 39, 15, 36 triangles (a 5, 12, 13 triangle enlarged by a factor of 3). The inradius in this case is 10.
For a general case, take two triangles 'back to back' with sides given by the primitive Pythagorean triple with m=x+1, n=x.
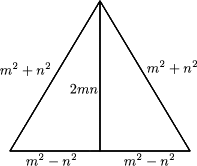
The radius of the incircle is given by:
As x, x+1 and 2x+1 are all relatively prime, if we enlarge the triangle by a factor x+1 taking m=(x+1)(x+1) and n=x(x+1) then the radius of the incircle of the new triangle will be the whole number
$ r=x(x+1)(2x+1).$As an example, for x=1, m=4, n=2, the isosceles triangle has sides of lengths 20, 20 and 24 (made up of two right angled triangles with sides of length 20, 16 and 12) and the inscribed circle has radius 6 units.
For another example take x=2, m= 9, n=6, then the isosceles triangle has sides of lengths 117, 117 and 90 (made up of two right angled triangles with sides of length 117, 108 and 45) and the inscribed circle has radius 30 units.
What happens for scalene triangles?