The Problem Imagine a rectangular tray lying flat on a horizontal table. Suppose that the tray has vertical sides, and that a plate (or disc) lies flat on the table and rolls around the outside of the tray in such a way that its circumference is always in contact with a side of the tray. What can we say about this motion? Now put the disc inside the tray and let the disc roll around inside the tray in contact with the side as it rolls around. What can we now say? In both cases the disc rotates as it rolls around and is not allowed to slide.

It will be helpful to think of the disc as a protractor marked, as usual, in degrees from 0 to 360. We say that the motion of the disc is periodic if the disc is in the same place, with the same angular mark at the point of contact at different times; if the motion is periodic then the motion keeps repeating itself over and over again. To get back to its starting position the disc has to rotate one or more complete revolutions and it has to travel around the tray one or more complete circuits. The number of circuits needed to get back to the starting position is called the period . In the two cases of the disc rolling outside and inside the tray, we shall explore conditions for the motions to be periodic.

First, we must understand the radian measure of an angle. Just as lengths can be measured in different units, say inches and centimetres, angles can also be measured in different units. If we know how long something is measured in one set of units we need to multiply this measurement by a fixed factor to find the length in the other set of units. For example, one inch is approximately 2.54 centimetres, so something of length 3.7 inches is also of length $3.7 \times 2.54 \ (9.398)$ centimetres.

We have the same situation for angles. We can either use degrees or radians as units, and the conversion factor here is such that 360 degrees is $2\pi$ radians so, for example 90 degrees is equivalent to $\pi/2$ radians.

The reason for introducing radians as units is to make the formula for the arc of a circle as simple as possible. The circumference of a circle of radius $r$ is $2\pi r$. The length of an arc of a circle that subtends an angle of $\theta$ radians at the centre of the circle is $r\theta$. If an arc subtends an angle of $\alpha$ degrees at the centre, then the length of the arc is the fraction $\alpha /360$ of the circumference, that is $2\pi r\times \alpha /360$ (a more complicated formula). Hence $\alpha$ degrees is $2\pi \alpha /360$ radians. For the rest of this article we shall work with radians rather than degrees. You can work in degrees and convert to radians if you wish, but this will involve you in more work and it is better to try and work in radians directly.

Rolling Outside

Let us look at a simple example. We shall suppose that the disc is of radius one, and that the tray is square with each side having an external measurement $s$. We shall think of the disc as a protractor. Suppose that the disc is in contact with the outside of the tray at the point $P$ of the disc (or protractor) marked $0$ degrees. What will be the mark on the protractor at the point $Q$ that is in contact with the tray after the disc has rolled once around the outside of the tray? The external perimeter of the tray is $4s$ so we get from $P$ to $Q$ by measuring a distance $4s$ around the circumference. Suppose $s= \pi/6$. Then $4s = 2\pi/3$ so that $Q$ is obtained from $P$ be measuring an arc from $P$ of length $2\pi /3$. This arc makes an angle of $2\pi/3$ radians (or $120^\circ$) at the centre so that $Q$ is at the point marked $120^\circ$. Similarly, if $s=5\pi/4$, then $Q$ will be the point marked $180^\circ$.

Now suppose that the tray has two sides of external length $a$ and two sides of external length $b$ (so the external perimeter is $2(a+b)$). What will be the mark at the point $Q$ in the following cases:

Example 1 $\quad a=b= \pi/2$;

Example 2 $\quad a=3\pi/4$ and $b=\pi/4$;

Example 3 $\quad a=5\pi/6$ and $b=\pi/6$?

How does the mark for $Q$ depend on the perimeter? Try to verify your answer for other values of $a$ and $b$.

The points $Q$ and $P$ come into contact with exactly the same point on the edge of the tray (so that the motion is periodic) if $Q$ and $P$ are actually the same point on the edge of the disc (at the $0^\circ$ mark). The disc may have rolled several times around the tray before $Q$ meets the tray at the same point as $P$ did. Suppose, for example, that $a=b=\pi$. Then after one revolution the position of the disc and tray will be indistinguishable from the starting position (and $Q$ will also be at the $0^\circ$ mark); we say that in this case the period is one. In each of the following cases find the smallest number of circuits around the tray before the point marked $0^\circ$ on the disc returns to the original starting position:

Example 4 $\quad a=\pi/2$ and $b= \pi/4$;

Example 5 $\quad a=\pi/2$ and $b= \pi/3$;

Example 6 $\quad a=\pi/3$ and $b= \pi/4$.

This number of circuits is the period of the motion.

Rolling Inside

What about the disc inside the tray? We may assume that the disc has radius $1$, and that the sides of the tray have internal lengths $2+a$ and $2+b$, where $a$ and $b$ are positive.

Let us look at a simple example. Suppose that the tray is square with each side having length $2+2\pi$, as in the following figure. On each side of the tray the disc rolls a distance of $2\pi$. As the length of the circumference of the disc is also $2\pi$ the point on the disc that is in contact with the point $A$ is the same as the point in contact with $B$. You should now convince yourself that if the disc starts at $A$ and rolls once around the tray, then when it is again in contact with $A$, the same point of the disc is in contact with $A$. The motion has period one.

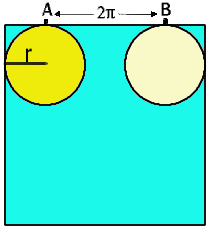
You should now check that the same situation holds whenever each side of the tray has length $2+2n\pi$, where $n$ is the same for opposite sides, but may be different for adjacent sides.

The tray measures $2 + a$ by $2 + b$. Can you describe the motion in the following examples? What is the period? If the disc rolls round and round for ever, do all the points on the rim of the disc come into contact with the edge of the tray?

Example 7 $\quad a=b=\pi/2$,

Example 8 $\quad a= 2\pi$ and $b=\pi/2$.

Now make up your own example; choose the period, then find the dimensions of a tray such that a disc of radius one unit rolling inside the tray has the period you have chosen.

Check your answers.