The Use of Mathematics in Computer Games : nrich.maths.org

'The Use of Mathematics in Computer Games' printed from http://nrich.maths.org/

Show menu

1 Introduction
2 First Person Shooters
- 2.1 Geometry, Vectors and Transformations
- 2.2 3D Graphics
3 Strategy Games
- 3.1 Nodes, Edges and Graphs
- 3.2 Path finding
4 Simulation Games
5 Conclusion
6 Answers
7 Interesting Web Pages

1 Introduction

The purpose of this article is to have a look at how mathematics is used in computer games. I'll use examples from computer games you've probably already played. There are lots of different types of computer games, and I'll talk about how maths is used in some of the following examples:

The First Person Shooter (FPS) is a type of game where you run around 3D levels carrying a big gun shooting stuff. Examples of this sort of game include Doom , Quake , Half Life , Unreal or Goldeneye . There are other games that look very similar, but aren't first person shooters, for instance Zelda: Ocarina of Time or Mario 64 .

The Strategy games are divided into two main types, Real Time Strategy (RTS), and Turn Based Strategy (not usually called TBS for some reason). These games usually involve building and managing a city or civilization and also fighting wars by controlling troops. Examples of real time strategy games are Age of Empires , Command &; Conquer , Tiberian Sun . Examples of turn based strategy games are Civilization and Alpha Centauri .

Simulation games are games that try to make something as realistic as possible. For instance, Flight Sims are computer games which try to realistically simulate flying an aeroplane or helicopter. Two games of this sort are Microsoft Flight Simulator and Red Baron . Space sims are like flight sims, but with spaceships instead of planes. For instance, Wing Commander or X-Wing vs. Tie Fighter . Racing games are games which simulate driving different sort of cars. For instance, Need for Speed , NASCAR Racing , Gran Turismo or Driver .

There are some exercises which you can do (if you want) throughout this article. The answers are at the end of the article, but do have a go at solving them on your own first. If there are any bits of this article you don't understand, you should either ask a question on the NRICH web board, or send an email to me at

dog@fcbob.demon.co.uk

If you find any of the article patronising, I apologise, my excuse is that the article is aimed at people of many different ages so there might well be bits you already know. If you already understand one bit, you can just skip through until you get to something more interesting.

2 First Person Shooters

The most amazing things about FPS are their incredible graphics. They look almost real, none of this would have been possible without the use of advanced maths. Here are some pictures from the early games (Wolfenstein) to the most recent games (Quake III Arena). All of the following screen shots are from games by iD software.

Wolfenstein, one of the earliest FPS games

Doom, the next breakthrough in graphics

Quake, this was a huge leap in the quality of graphics in computer games

Quake III, one of the newest FPS games around

To begin to explain how these games work, you need to know a bit about geometry , vectors and transformations .

2.1 Geometry, Vectors and Transformations

Geometry is the study of shapes of various sort. The simplest shape is the point . (It's quite difficult to explain what a point is, it is basically just a position, for instance, the very end of your nose is a point). Another simple shape is a straight line . A straight line is just the simplest shape joining two points together. A plane is a more complicated shape, it is a flat sheet, like a piece of paper or a wall. There are more complicated shapes, called solids , like a cube or a sphere. Here are some pictures of these things.

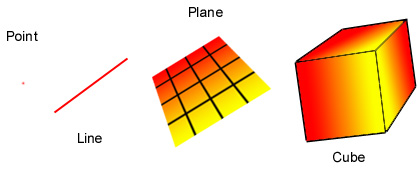
Simple geometric figures

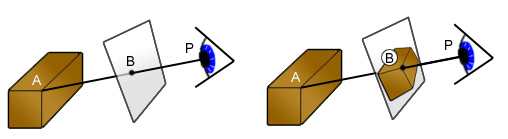
If you have a line and a plane, you can find the point where the line cuts through the plane. In fact, sometimes you can't find the intersection, because they don't meet and sometimes the line is inside the plane so they meet at every point on the line , but this doesn't happen in the cases we're interested in. We call this the intersection of the line and the plane. Here is a picture of what this looks like.

Intersection of a line and a plane

A vector is a mathematical way of representing a point. A vector is 3 numbers, usually called $x$, $y$ and $z$. You can think of these numbers as how far you have to go in 3 different directions to get to a point. For instance, put one arm out pointing to the right, and the other pointing straight forward. I can now give you a vector and you'll be able to find the point I'm talking about. For instance, if I say $x=3$, $y=1$, $z=5$, you find the point by walking 3 metres in the direction of your right hand, then 1 metre in the direction of your left hand, and then getting a ladder and climbing up 5 metres. Here is a picture of a vector.

Picture of a vector and directions

Vectors are written as $(x,y,z)$, for instance $(1,2,3)$ means move 1 in the x-direction, 2 in the y-direction and 3 in the z-direction.

One confusing thing about vectors is that they are sometimes used to represent a point, and sometimes they are used to represent a direction. The vector $(1,0,0)$ can mean both ``the point you get to if you move 1 unit in the x-direction from the starting point'', or it can mean ``move 1 unit in the x-direction from where you are now''.

Exercise 1 [Adding Vectors]

If I start at the point represented by the vector $(0,0,0)$, then I travel along the vector $(1,2,3)$, and then I travel along the vector $(4,5,6)$, where will I be? This vector is called the sum of the two vectors, $(1,2,3)+(4,5,6)=(?,?,?)$.

A transformation moves a point (or an object, or even an entire world) from one place to another. For instance, I could move it to the right by 4 metres, this type of transformation is called a translation . Another type of transformation is rotation . If you take hold of an object (a pen for instance), and twist your wrist, you have rotated that object. Here are some pictures of rotations and translations.

Translations and rotations

Exercise 2 [Translations]

If I translate the vector $(1,2,3)$ by 5 in the y-direction, what is the vector afterwards? In general, if we write a translation as $T$ and a vector as $\mathbf{v}$, then the new vector if written as $T\mathbf{v}$. For example, if $T$ is ``translate 1 unit in the x-direction'' and $\mathbf{v}=(0,0,0)$, then $T\mathbf{v}=(1,0,0)$.

2.2 3D Graphics

The basic idea of 3D graphics is to turn a mathematical description of a world into a picture of what that world would look like to someone inside the world. The mathematical description could be in the form of a list, for instance: there is a box with centre $(2,4,7)$ and sides of length 3, the colour of the box is a bluish grey . To turn this into a picture, we also need to describe where the person is and what direction they are looking, for instance: there is a person at $(10,10,10)$ looking directly at the centre of the box . From this we can construct what the world would look like to that person.

Imagine there is a painter whose eyes are at the point $P$. Imagine that he has a glass sheet which he is about to paint on. In the room he is painting, there is a wooden chest. One of the corners of the chest is at point $A$, and the painter wants to know where that corner of the chest should be on his glass sheet. The way he works it out is to draw a line $L$ from his eyes ($P$) to the corner of the chest ($A$), then he works out where this line goes through the canvas, $B$. He can do this, because the glass sheet is a plane, and I mentioned that you can find the intersection of a line and a plane above. This point $B$ is where the corner of the chest should be in his painting. He follows this rule for every bit of the chest, and ends up with a picture which looks exactly like the chest. Here are two pictures, the first one shows the painting when he has only painted the one corner of the chest, the second one shows what it looks like when he has painted the entire chest.

Projection on to a plane

What I just described above is similar to what the computer is doing (50 times a second!) every time you run around shooting hideous monsters in Quake , although the details are slightly different. In computer games (at the moment) the description of the world is just a list of triangles and colours. The newest computer games are using more complicated descriptions of the world, using curved surfaces, NURBS and other strange sounding things, however in the end it always reduces to triangles. For instance, a box can be made using triangles as illustrated below.

Box made from triangles

Here is a much more complicated example, using thousands of triangles. The first picture shows the triangles used, the second picture is what it looks like with colours put in.

Viking Helmet

The reason for using triangles is that they are a very simple shape, and if you make sure that everything is made from only one type of shape, you don't have to write a separate program for each type of shape in the game.

Exercise 3 [Making triangles] Draw a picture of a box with a smaller box stuck to the top of it, using only triangles.

Each time the computer draws a picture of the world, it goes through the following steps: Firstly, it transforms the world (by rotating and translating), so that the person is at position $(0,0,0)$ and the centre of the glass sheet (the centre of the screen in computers) is at $(1,0,0)$. This makes the rest of the calculations much easier. Secondly, it removes all the triangles you can't see so that it can forget about them, for instance the triangles that are behind you or the ones that are so far away that you can't see them. Thirdly, for every remaining triangle, it works out what it would look like when painted on the glass sheet (or drawn on the screen in computers). Finally, it puts the picture it has drawn on the screen. Nowadays, computers are so fast that they can draw hundreds of thousands of triangles every second, making the pictures more and more realistic, as you can see from the pictures at the beginning of this section.

Of course, there is a lot more to it than just that: there is lighting, fog, animation, textures and hundreds of other things. Most of these use maths and physics to a large extent, but what I have described so far is the most important part of making 3D graphics look right.

3 Strategy Games

Strategy games usually have much simpler graphics than FPS games, so I'm going to talk about some other interesting bits of strategy games. When you click on a little soldier in a strategy game, and then click somewhere else, telling him that he should walk to the place where you have clicked, what happens inside the computer? How does the computer know how to make the soldier get from where he already is to where he is going. Remember, computers can't think for themselves (yet!), they need to be told exactly what to do. So you can't just say, ``look at the map and work out the best route to wherever you are going'', he needs to be given exact instructions at every stage of his journey. This problem is called path finding , and this is what I'm going to talk about in this section.

3.1 Nodes, Edges and Graphs

To explain how the computer works out the best route, you need to know what nodes , edges and graphs are. You may have heard of graphs before in maths, but they mean something slightly different here. The simplest example of nodes and graphs is a map of some cities, and the roads between them (or an underground map). Each city is a node, usually drawn as a circular blob. Each road is an edge, and connects two nodes (cities), these are usually drawn as straight lines. The whole collection of nodes and edges (cities and roads) is called a graph. Sometimes there is a one way road, called a directed edge , and we draw an arrow on it to show which way you can travel along it. For instance, if there are two cities $A$ and $B$, and a line with an arrow from $A$ to $B$, then we can travel from $A$ to $B$, but not from $B$ to $A$. Here is an example of a graph, you can't travel from $B$ to $A$, but you can travel from $A$ to $B$. You can't travel from $C$ to $A$ or from $A$ to $C$, but you can travel from $B$ to $C$ and from $C$ to $B$.

Graph with directed edges

To complicate things even further, we sometimes want to add something called a cost to each edge. The idea of a cost is that it indicates how much it would cost to travel down that edge. A simple example of this is shown below.

Graph with costs

In this graph, most of the people in city $A$ want to get to city $C$, whereas only a few want to get to city $B$. Unfortunately, both roads are the same size, this means that there are long traffic jams on the road from $A$ to $C$, it takes about 30 minutes to get there. To get from $A$ to $B$ is much easier as most people are going to $C$, so it only takes 5 minutes. The numbers written next to the edges indicate how long it takes to travel along that edge. Here is another (much more complicated) example.

More complicated graph

Exercise 4 [Shortest Path] Work out the lowest cost way to get from A to K .

3.2 Path finding

Now you know all you need to know to be able to understand path finding. If you did the last exercise, you'll have already solved one example of the sort of problem computers have to solve to guide troops through complicated maps.

How does all this stuff about graphs help the computer guide troops around levels? It makes a graph where every interesting point is a node on the graph, and every way of walking from one node to another is an edge, then it solves the problem you solved above to guide the troops. There are some complications. For starters, what are the interesting points? You might think that every position on the entire level is interesting, but for most games this would lead to hundreds of thousands of interesting points, and finding the path would take years. Instead, the people making the game decide where the interesting points are. For instance, if there is a wide open expanse (a big field perhaps), you don't need a node at every point on the field, because the troops can walk in a straight line across the field. Basically, you only need nodes around obstacles. Here is an example of a map of a level seen from above.

A map of a level in a game, the green areas are the ground, the grey areas are the buildings

Once you have chosen your interesting points, you need to connect them up with edges, you can only connect up those nodes which don't have an obstacle between them.

Exercise 5 [Make your own graph] Place nodes at the interesting points on the example map above, then connect up the nodes with edges, remembering that you can only connect up nodes with straight lines, and the straight lines cannot go over obstacles.

Once you have created a graph for a given map, the computer has to go through the following steps to guide the troops. Firstly, it has to work out what the nearest node that he can walk to in a straight line. This node is his starting node. Secondly, he has to work out the node which is nearest to his destination is (making sure he can walk from that node to the destination in a straight line of course!). This node is the destination node. Thirdly, he works out the shortest path connecting his starting node to his destination node. Now, all the troops have to do is walk to the starting node, then walk along all the nodes between the starting node and the destination node, along the connecting edges, then they walk from the destination node to the final destination.

To make things a bit more interesting, we can add costs to all of the edges. For instance, if there is a crocodile pit in the space connecting two nodes, the cost of crossing this crocodile pit is very high, so it might be a better idea to go the long way round even though crossing the crocodile pit is shorter. Of course, if the long way round would take the troops 3 days, and crossing the crocodile pit only took 15 minutes, they might decide that it would be better to take the risk and get there before the battle has moved elsewhere. You have to choose the costs carefully to make sure this sort of problem is solved in the best possible way. Here is an example of a map with edges with costs.

I haven't actually talked about how to get a computer to find the best path from one node to another yet. The total cost of getting from $A_1$ to $A_m$ via $A_2$, $A_3$, ..., $A_{m-2}$, $A_{m-1}$ is found by adding up the cost of going from $A_1$ to $A_2$, $A_2$ to $A_3$, ..., $A_{m-1}$ to $A_m$. The problem is to find the right choice of nodes that this total cost is as small as possible. One way of doing it would be to find all possible ways of getting from one node to the other, work out the total costs of each, and choose the smallest one. Unfortunately, this would take even the fastest computers much too long to do. There is a way of working this route out very quickly, but it is a bit complicated to explain here. However, if you're keen, you can look it up on the internet (search for the A* Algorithm - A* is pronounced A star), or you can check out the references at the end of the article.

4 Simulation Games

The most important thing about simulation games is that they try and make the game like the real world. Usually this involves physics simulation . This section might be a bit hard if you haven't done any physics at school, but here goes.

4.1 More on Vectors

Physics used in computer games uses vectors. There a few more things you need to know about vectors. Firstly, instead of writing $(x,y,z)$ every time we talk about a vector, we'll just write $\mathbf{v}$ for a vector, this is the same as writing $(v_x,v_y,v_z)$. When I write $v_x$, that just means the distance you have to go in the x-direction to get to $\mathbf{v}$. We can add two vectors $\mathbf{v}+\mathbf{w}=(v_x+w_x,v_y+w_y,v_z+w_z)$. We can multiply a vector by a number, $a\mathbf{v}=(a v_x, a v_y, a v_z)$. For instance, $3 \times (1,2,3)=(3,6,9)$. The length of a vector is the length of the line from $(0,0,0)$ to the vector, the length is written $|\mathbf{v}|$, and you can work it out using the formula $|\mathbf{v}|=\sqrt{v_x^2+v_y^2+v_z^2}$. For example, $|(1,2,2)|=\sqrt{1^2+2^2+2^2}=\sqrt{9}=3$. The length of a vector multiplied by a (positive) number is the number times the length of the vector, so $|a\mathbf{v}|=a|\mathbf{v}|$.

Exercise 6 [Vectors]

(a) What is (1,2,3)+(3,2,1)?

(b) What is 10x(9,5,2)?

(c) What is the length of (4,2,4)?

4.2 Physics

Every object has a position , which is a vector $\mathbf{x}$. It also has a velocity , which is the direction it is travelling in, it is also a vector $\mathbf{v}$, sometimes written as $\mathbf{\dot{x}}$. Every object also has something called an acceleration , this is how fast the velocity is changing, and it is also a vector $\mathbf{a}$, sometimes written as $\mathbf{\ddot{x}}$. Finally, every object has something called mass , this is basically how heavy the object is, and is usually written $m$, but this is not a vector. If an object starts at position $\mathbf{x}$, and has a velocity $\mathbf{v}$ which doesn't change, then after $t$ seconds, the position of the object is $\mathbf{x}_t=\mathbf{x}+\mathbf{v}\times t$. In case you're wondering what $\mathbf{x}_t$ means, it just means the position at time $t$. Similarly, $\mathbf{v}_t$ means the velocity at time $t$. If an objects starts with velocity $\mathbf{v}$ and has an acceleration $\mathbf{a}$ which doesn't change, then after $t$ seconds, the velocity of the object is $\mathbf{v}_t=\mathbf{v}+\mathbf{a} \times t$.

Here is an example of how to use this to work something out. Suppose Billy-Joe Bob is floating in space, his position is $(100,150,150)$ and he throws a rock with velocity $(5,2,0)$. Where is the rock after 10 seconds? To work this out, we use the formula above: $\mathbf{x}_t=\mathbf{x}+\mathbf{v}\times t$. In this case (after 10 seconds) the rock is at $(100,150,150)+(5,2,0)\times 10=(100,150,150)+(50,20,0)=(150,170,150)$.

Exercise 7 [Throwing Rocks in Space] Billy-Joe's mortal enemy, Arthur Blenkinsop is at (240,640,143), reading his newspaper, unaware that Billy-Joe is watching him. Billy-Joe decides to throw his rock at Arthur. Billy-Joe is slightly obsessed with the number 7, so he wants the rock to take exactly 7 seconds to reach Arthur, what velocity should he throw the rock at?

If Billy-Joe wasn't in space, the problem would be much harder, because every object on Earth is pulled downwards by an acceleration caused by gravity . This acceleration is the same for every object on Earth, and if the y-direction is upwards, then the acceleration is $\mathbf{g}=(0,-9.81,0)$. The reason the problem is now harder is that the velocity changes, so you can't use the equation above to work out the position at different times. If we have a computer, we can work out things like this, but not exactly. The way we do it is by saying that the velocity is only changing very slightly over very small amounts of time. For instance, the velocity only changes by a very small amount in 0.02 seconds. So, we can work out what happens for very small amounts of time, if $s$ is very small, maybe $s = 0.02$, the equation $\mathbf{x}_{t+s}=\mathbf{x}_t+\mathbf{v}_t \times s$ is very close to being correct. In that equation $\mathbf{x}_{t+s}$ is the position at time $t+s$, $\mathbf{x}_t$ is the position at time $t$, $\mathbf{v}_t$ is the velocity at time t which we can work out because the acceleration doesn't change. By doing this repeatedly, we can get a computer to work out where the rock will be at any time, by working out where it will be after 0.02 seconds, then after 0.04 seconds, then after 0.06 seconds, and so on until we get to the time we want.

Exercise 8 [Throwing Rocks on Earth] Billy-Joe is at position (0,0,0), he throws a rock with velocity (0,4,0), where will the rock be after 1 second? To answer this question, the acceleration on the rock is (0,-9.81,0), and you should use s = 0.2, you will need to use the method above 5 times to work it out. You might like to see if you can work out how long it takes for the rock to hit him on the head.

4.3 Simulation Games

How is all this stuff actually used in computer games? Here's a simple example. Every time you fire a bullet from your plane in your favourite flight simulator, the computer has to work out its position using calculations like the ones above with Billy-Joe throwing rocks around. The computer has to do these calculations 50 times a second for every bullet in the sky, and on top of that it has to do much harder calculations for the planes as well. Unfortunately, things are not as easy as working out where Billy-Joe's rocks are. It is much more complicated, because in the real world, there are things like wind and friction because of the air. Here is how you might include wind in the calculations. Suppose the wind causes the bullet to have an additional acceleration of $\mathbf{w}$, and the wind is blowing at a constant rate (the wind speed isn't changing). Now we have the acceleration on the bullet is $\mathbf{g}+\mathbf{w}$, which isn't that much more complicated than before. Friction in the air is much more complicated though, because the amount of friction depends on the speed of the bullet. In fact, the friction causes an additional acceleration of $-k\mathbf{v}$, where $k$ is some positive number and $\mathbf{v}$ is the velocity. So now the acceleration is $\mathbf{g}+\mathbf{w}-k\mathbf{v}$: in other words, the acceleration is changing as well as the velocity! This problem can be solved using the method above, where you assume that things don't change in small periods of time.

For the plane, things are even more complicated. If you fly your plane as high as it will go and then go into a nose dive, you might find that the wings of your plane rip off (if you are playing a flight simulator with new planes this might not happen, because planes are better now than they used to be). This happens because the air pushes the wings very hard, and they are not attached strongly enough to the rest of the plane, so they just rip off.

Physics is one of the hardest bits in making computer games. Few games have accurate physics, most games only have something about as complicated as what I described above. It is such a hard problem that people are researching into how to simulate realistic physics in computer games even now, and they're quite a long way from the solution. So if you're interested in programming games and you're interested in physics, then you might even find yourself working on this problem in years.

5 Conclusion

I've shown you quite a few examples of where maths is used in making computer games, there are many, many more examples. In fact, it is almost impossible to make any game without using maths, even Pacman uses some maths (although it is quite easy maths compared with the hard stuff in this article). If you have any questions about this article, you should post any questions to the NRICH web board, or email them to me at dog@fcbob.demon.co.uk

. You should also post if you would like to ask me (or the others) about how maths is used in any other part of making computer games.

6 Answers

Answer to Question 1 [Adding Vectors]

The answer is $(1,2,3)+(4,5,6)=(5,7,9)$. This is because $1+4=5$, $2+5=7$ and $3+6=9$. The reason the answer is those sums is because to find out how far we go in the x-direction, we work out how far we have gone in the x-direction from the first vector, and add on how far we have gone in the x-direction from the second vector. We do the same for the y- and z-directions. In general, $(x,y,z)+(u,v,w)=(x+u,y+v,z+w)$.

Answer to Question 2 [Transformations]

The answer is $(1,7,3)$ because we add the vector $(0,5,0)$ to move 5 in the y-direction, and $(1,2,3)+(0,5,0)=(1,7,3)$. In general, a translation $T$ is something like ``add $(u,v,w)$ to the vector'', to $T(x,y,z)=(x,y,z)+(u,v,w)=(x+u,y+v,z+w)$. If you haven't done matrices and vectors at school, ignore the next bit.

To rotate a vector by an angle $\theta$ about the x-axis, the matrix is

\mathbf{M}_{\theta} = \left( \begin{array}{ccc} \cos(\theta) & -\sin(\theta) & 0 \\ \sin(\theta) & \cos(\theta) & 0 \\ 0 & 0 & 1\\ \end{array} \right)

So
$\mathbf{M_{\theta(x,y,z)}}=(x\cos(\theta)-y\sin(\theta),x\sin(\theta)+y\cos(\theta),z)$.

Answer to Question 3 [Making triangles] Here is one way of doing it, but not the only way:

Two boxed attached, drawn with triangles

Answer to Question 4 [Shortest Path]

The shortest way to get from $A$ to $K$, is to go $A B C H G J K$.

Answer to Question 5 [Make your own graph] Here is one way to do it, but this isn't necessarily the only way to do it.

Level map with graph

If you are creating random levels in a game, you can't decide on where the interesting points are, so you need to think of a way to instruct the computer to decide where the interesting points are. There are lots of ways of doing this, think about how you might go about doing this. Some things to consider are (a) can you get to every point on the map by walking in a straight line from some node? You need to make sure you can. (b) Do you have any silly situations, like the one below where you can get from A to B, but only by taking a very silly route.

A very silly choice of graph

Answer to Question 6 [Vectors]

(a) $(1,2,3)+(3,2,1)=(4,4,4)$.

(b) $10\times (9,5,2)=(90,50,20)$.

(c) $|(4,2,4)|=\sqrt{4^2+2^2+4^2}=\sqrt{16+4+16}=\sqrt{36}=6$.

Answer to Question 7 [Throwing Rocks in Space]

Write Billy-Joe's position as $\mathbf{x}$ and Arthur's position as $\mathbf{y}$. If Billy-Joe throws the rock with velocity $\mathbf{v}$, then after $t$ seconds, the rock will be at $\mathbf{x}+\mathbf{v}\times t$. He wants it to hit Arthur, so he wants $\mathbf{x}+\mathbf{v} \times t = \mathbf{y}$. Rearranging this equation, we get $\mathbf{v}=\frac{\mathbf{y}-\mathbf{x}}{t}$. So, the velocity should be the position of Arthur minus the position of Billy-Joe, divided by the time taken, 7 seconds. So $\mathbf{v}=\frac{(240,640,143)-(100,150,150)}{7}=\frac{(140,490,-7)}{7}=(20,70,-1)$.

Answer to Question 8 [Throwing Rocks on Earth]

Because the x- and z-directions are 0 in all the vectors, we can ignore them and just look at the y-directions. At time $t=0$, the rock is at position 0, with velocity 4 (with vectors, the rock is at position $(0,0,0)$ with velocity $(0,4,0)$). Therefore, at time $t=0.2$, the rock will be at position $0+4 \times 0.2=0.8$. At time $t=0.2$, the velocity will now be $4+0.2 \times -9.81 = 2.038$. So, at time $t=0.4$, the rock will be at position $0.8+2.038 \times 0.2=1.2076$. At time $t=0.4$, the velocity will be $4+0.4 \times -9.81=0.076$. So at time $t=0.6$, the rock will be at $1.2076+0.076 \times 0.2 = 1.2228$. At $t=0.6$, the velocity will be $4+0.6 \times -9.81 = -1.886$, so at $t=0.8$ the position will be $1.228-1.886 \times 0.2 = 0.8508$. At $t=0.8$ the velocity will be $4+0.8 \times -9.81 = -3.848$, so at $t=1.0$ the position will be $0.8508-3.848 \times 0.2 = 0.0812$. So, after 1 second, the position of the rock will be $(0,0.0812,0)$.

For the last part of the question, you work out the velocity at time $t=1.0$ is $4-9.81 \times 1.0 = -5.81$, so the position at time $t=1.2$ is $0.0812-5.81\times 0.2=-1.0808$, so somewhere between $t=1.0$ and $t=1.2$, the rock hits Billy-Joe on the head.