Many of you will remember a problem entitled "Score" which recently appeared in the June Six. Class 2YP from Madras College was inspired by this to work out in how many ways the number 1999 could be expressed as the sum of 3 odd numbers, and this is their solution.

We decided to investigate the number of different ways various totals may be obtained by adding small numbers of odd numbers. Systematic working led us to consider the cases: 1 odd number, 2 odd numbers, 3 odd numbers.

1 odd number

There was unanimous agreement! Each of the totals 1,3,5,7,... can be obtained in only one way. The pattern is:

1,1,1,1,1,1,1,......

with repeating block [1].

2 odd numbers

Eventually there was unanimous agreement:

						Totals:	2	4	6	8	10	12	14
						Ways:	1+1	3+1	5+1	7+1	9+1	11+1	13+1
									3+3	5+3	7+3	9+3	11+3	etc...
											5+5	7+5	9+5
													7+7
						No. of Ways:	1	1	2	2	3	3	4

and a repeating block pattern emerges. In this case the 1st differences are repeated:

	1		1		2		2		3		3		4	...
		0		1		0		1		0		1	...

with repeating block in the 1st differences of [01].

3 odd numbers

There was some agreement and much confusion. What emerged was the following:

							Totals:	3	5	7	9	11	13	15
							Ways:	1+1+1	3+1+1	5+1+1	7+1+1	9+1+1	11+1+1	13+1+1
										3+3+1	5+3+1	7+3+1	9+3+1	11+3+1
											3+3+3	5+5+1	7+5+1	9+5+1
												5+3+3	7+3+3	9+3+3
													5+5+3	7+7+1
														7+5+3
														5+5+5
								No. of Ways :	1	1	2	3	4	5	7

There was initial excitement when 1,1,2,3,... emerged and Fibonacci's name was bandied about.

By the time 1,1,2,3,4,5,... was reached the initial 1 was being viewed as a "rogue" value and most of the class were in agreement with 6,7,8,... being the continuation. There was great consternation when 7 emerged and not 6.

Eventually this pattern emerged:

	1		1		2		3		4		5		7		8		10		12		14		16		19		21		24		27		30
		0		1		1		1		1		2		1		2		2		2		2		3		2		3		3		3
			1		0		0		0		1		-1		1		0		0		0		1		-1		1		0		0

and so the conjecture emerged that there was a repeating block in the 2nd differences of [1,0,0,0,1,-1].

The question was now asked:
" In how many ways can 1999 be written as the sum of three odd numbers? "

Agreement was reached that continuing the pattern to reach 1999 was not feasible!

A fresh look at the block structure:...

		3		5		7		9		11		13					15		17		19		21		23		25					27		29	...
	----------------------																--------------------------														---------
		1		1		2		3		4		5					7		8		10		12		14		16					19		21	...
			0		1		1		1		1		2					1		2		2		2		2		3					2		3	...
				1		0		0		0		1		-1					1		0		0		0		1		-1					1		0	...
				-------------------------																--------------------------														---------
						B	L	O	C	K		1											B	L	O	C	K		2

raised a new question: In which block is 1999?

The first "total" in each block gives

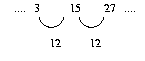
So comparing with the multiples of 12 ... 12, 24, 36, ... gave us the formula 12n-9 for the first "total" on block n.

Now 12n-9=1999 => 12n=2008 => n=167.333...


So 1999 is in the 167th block. 12 * 167 - 9 = 1995 gives :

1995		1997		1999	...
-	-	-	-	-	-	-	-
?
	166		167		167	...
		1		0		0	...
-	-	-	-	-	-	-	-

Block 1		Block 2		Block 3		Block 4	...	Block 167
-	-	-	-	-	-	-	-	-
1		7		19		37	...	?
	6		12		18	...
		6		6	...

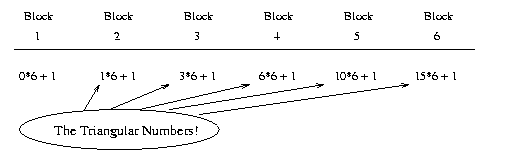
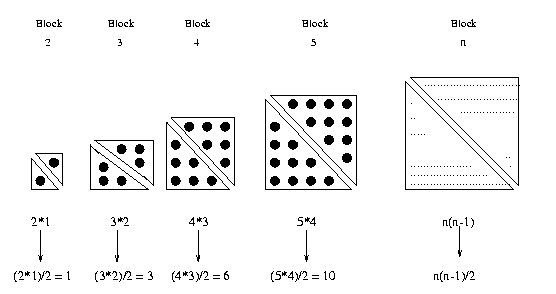
$6n(n-1)/2 + 1$
$= 3n(n-1) + 1$
$= 3n^2 - 3n + 1$

In particular when $n=167$ this gives $3*167^2 - 3*167 + 1 = 83167$

1995		1997		1999
-	-		-	-	-	-	-
83167		83333		83500	...
	166		167		167	...
		1		0		0	...
-	-	-	-	-	-	-	-