Copyright © University of Cambridge. All rights reserved.
'The Frieze Tree' printed from https://nrich.maths.org/
Show menu
Sorting friezes
Repeating strip patterns, called friezes, occur all over the world in border decoration in buildings, textiles etc. All frieze patterns have a section of the pattern which is repeated alongside itself (we call this a translation). In distinguishing one frieze pattern from another we first need to find the smallest translation length in the strip. This defines the 'cell' which is the smallest piece of the pattern to be repeated by translations. Perhaps surprisingly mathematicians say that there are only seven different frieze patterns. This article first gives a simple way of sorting friezes into the seven types and then explains why there are only seven.
Apart from translation, there are four other symmetries which transform the strip into itself. We shall call the four symmetries H, V, R and G: that is H for reflection in a mirror line along the strip (horizontal reflection, a symmetry which occurs in the letter D); V for reflection in a mirror line perpendicular to the strip (vertical reflection, as in A); R for rotation by a half turn (as in the letter S); and G for a glide reflection (as in bp). Frieze patterns are classified according to whether each of the four symmetries do or do not occur, and you can use a decision tree to do this classification.
[Some words of warning: There may be other symmetries within the cell (such as quarter turns or enlargements) but these symmetries should not be taken into account because they do not transform the whole strip into itself. For example in the pattern EE EE EE EE E the enlargement does not map the whole strip into itself and this is counted as the same frieze type as FFFFFFFFF. Also when you look for glide reflections they must be within the cell which means that the translation length of the glide reflection must be one half of the translation length mapping one cell to the next. Strips like DDDDDDDDD or HHHHHHHHH have glide reflections from one cell to the next but not within the cell.]

How many different types of frieze pattern would you expect? You might reasonably expect 2x2x2x2 or sixteen but there are just seven ways of `transforming' a frieze pattern so that it is indistinguishable from the original, that is only seven pattern types. If you don't believe this then try using the tree to classify your patterns and you will only ever end up with one of seven.
The list below gives the classification of the seven frieze pattern types.
| Type 1: p111 | FFFFFF - translations only |
| Type 2: pm11 | AAAAA - translations and vertical reflections |
| Type 3: pmm2 | HHHHH - translations, vertical and horizontal reflections and half turns |
| Type 4: p1a1 | bpbpbpb - translations and glide reflections |
| Type 5: pma2 | bpqdbpq- translations, vertical reflections, glide reflections and half turns |
| Type 6: p112 | SSSSSSS - translations and half turns |
| Type 7: p1m1 | DDDDD - translations and horizontal reflections. |
You might like to use the decision tree to sort the patterns from Heather McLeay's article Frieze Patterns in Cast Iron .
Constructing friezes
What we have looked at so far is how to sort frieze patterns into different types. Now let us consider constructing frieze patterns.
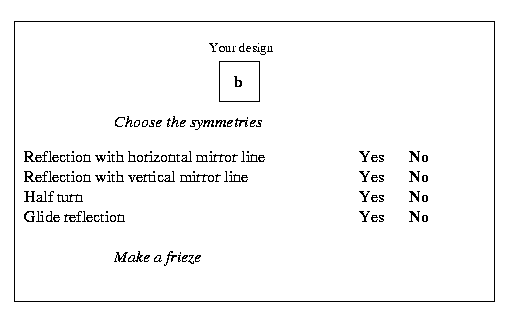
Let's start with a cell with a letter b in it. You may like to make some friezes using the letter b and different combinations of the four symmetries and explore the different possibilities.
Suppose we could switch the symmetries on and off by selecting 'Yes' and 'No' for each one and then make the corresponding friezes. We could choose any of the sixteen combinations of H (reflection with a horizontal mirror line), V (reflection with a vertical mirror line), R (half turn) and G (glide reflection). Then for example choosing NNNY would give a frieze of type 4, as described earlier, which does not have H, V or R symmetries but does have G symmetries.
If you choose four 'Nos', or three 'Nos' and one 'Yes', nothing unexpected happens. You get the following frieze patterns. You can imagine the pattern on a strip of elastic which can be stretched or contracted to make the pattern look more attractive without altering the combination of symmetries in the pattern.
|
|
|
b b b b b b b b b b b b b b b |
NNNN - Type 1: translations only. |
|
|
|
|
|
|
b b b b b b b b b b b b b b b |
YNNN - Type 7: translations and horizontal reflections. |
p p p p p p p p p p p p p p p |
|
|
|
|
|
|
|
b d b d b d b d b d b d b d |
NYNN - Type 2: translations and vertical reflections. |
|
|
|
|
|
|
b b b b b b b b b b |
NNYN - Type 6: translations and half turns. |
d d d d d d d d d d |
|
|
|
|
|
|
|
b b b b b b b b b b |
NNNY - Type 4: translations and glide reflections. |
p p p p p p p p p |
|
|
|
So far this accounts for five of the sixteen combinations. It is when you try to have two of the four symmetries (two 'Yes' and two 'No') that you find it becomes impossible and that by selecting two symmetries a third one is always introduced into the pattern. The third symmetry is a combination of the other two.
If you choose two reflections you automatically get a half turn (accounting for two more combinations YYNN and YYYN) and if you choose either reflection, but not the other, together with a half turn, you automatically get the other reflection (accounting for two more combinations YNYN and NYYN, nine of the sixteen so far).
|
|
|
b d b d b d b d b d b d b d b d |
Type 3: translations, vertical and horizontal reflections and half turns. |
p q p q p q p q p q p q p q p q |
|
|
|
If you choose a vertical reflection and a glide you automatically get a half turn (accounting for two more combinations NYNY and NYYY). Although the resulting pattern will not look quite the same if you choose a half turn and a glide you automatically get a vertical reflection and a frieze pattern of the same type (accounting for another combination NNYY, twelve out of sixteen so far).
|
|
|
b d b d b d b d b d b d b d b d |
Type 5: translations, vertical reflections, glide reflections and half turns. |
p q p q p q p q p q p q p q p q |
|
|
|
At this point we have got all seven frieze patterns. We have seen that pairs of symmetries combine to produce a third symmetry so we can have one or three but not two of the four symmetries in the pattern. We still have to account for four more of the combinations and explain why it is impossible for all four symmetries to occur.
If we have both a horizontal and a glide reflection (YNNY) we get the following 'cell', but this introduces a translation inside the cell itself so, as the frieze is derived from repetition of the smallest translation length, there is automatic cell division giving two new cells. However there is no glide reflection within these second generation cells. Altogether this accounts for thirteen out of the sixteen combinations, but does not give a new frieze pattern.
|
|
|
b b |
|
p p |
|
|
|
The corresponding frieze pattern is one which occurred earlier.
|
|
|
b b b b b b b b b b b b b b b |
Type 7: translations and horizontal reflections. |
p p p p p p p p p p p p p p p |
|
|
|
A similar thing happens when you try to put in all four symmetries (YYYY). Starting with a 'b' together with horizontal and vertical reflections and half turns, then selecting glide reflections as well, gives the following 'cell'.
|
|
|
db db |
|
qp qp |
|
|
|
However this introduces a translation inside the cell itself so there is automatic cell division again, giving two new cells. There is no glide reflection within these second generation cells. This accounts for fourteen out of the sixteen combinations but does not give a new frieze pattern
|
|
|
db db db db db db db db db db |
Type 3: translations, vertical and horizontal reflections and half turns |
qp qp qp qp qp qp qp qp qp qp |
|
|
|
The two remaining combinations (YYNY and YNYY) would produce the same result as YYYY and again a type 3 pattern, but they never occur. The first YYNY and can only come about following YYNN or YNNY or NYNY or YYYY but we have shown that none of these occurs and YNYY can only come about following NNYY, YNNY, YNYN or YYYY and we have shown already that none of these occurs.
In the next article we shall introduce an algebra for the group of symmetries in the frieze patterns and show how the symmetries combine.