In the article Magic Squares we saw how to construct at least one magic square of any order. We can use some properties of magic squares to transform our manufactured square into many different magic squares. Some of the properties of magic squares are:

 

1. A magic square will remain magic if any number is added to every number of a magic square.
2. A magic square will remain magic if any number multiplies every number of a magic square.
3. A magic square will remain magic if two rows, or columns, equidistant from the centre are interchanged.
4. An even order magic square ($n\times n$ where $n$ is even) will remain magic if the diagonally opposite quadrants are interchanged.
5. An even order magic square will remain magic if the columns or the rows are exchanged. If the 1^st and the 2^nd columns/rows are exchanged and the 3^rd and the 4^th columns/rows are exchanged, this is called a 1-2-3-4 exchange.

The first two properties would yield an infinite number of magic squares since there are an infinite number of numbers we could add to every number or multiply every number by to produce a different magic square. How boring, so let's restrict our search for different magic squares to just those that use the integers from $1$ to $n$, for an $n\times n$ square. Also, let's not consider squares obtained only by rotation and/or reflection, for they are just a different view of the same square. That will leave us to first consider property number 3:

3. A magic square will remain magic if two rows, or columns, equidistant from the centre are interchanged.

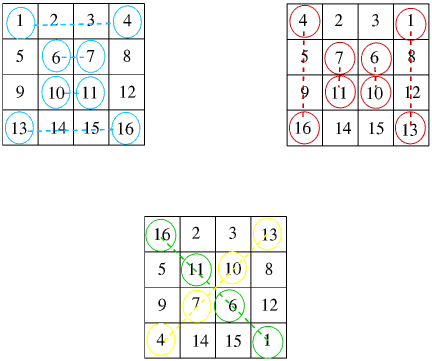
Let's consider only even number magic squares at first and see the squares produced. Below, I have used this property to produce 9 different squares and illustrate how the rows and columns may be interchanged.

 

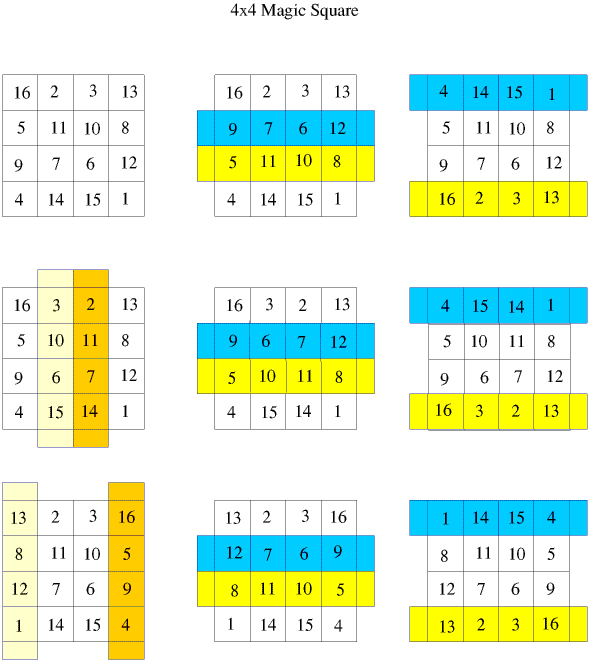
The middle magic square on the middle row is the famous Durer "Melancholia'' with its date of 1514 on the bottom line. You can see a picture of the engraving at the site:
https://mathshistory.st-andrews.ac.uk/Biographies/Durer/ .
We will see this square again.

 

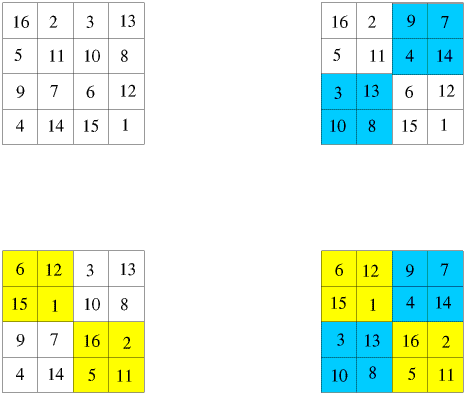
Now let's consider the fourth transformation property of magic squares:

4. An even order magic square ($n\times n$ where $n$ is even) will remain magic if the quadrants are interchanged.

Again, I have used this property to produce different squares and illustrate the method of transformation.

 

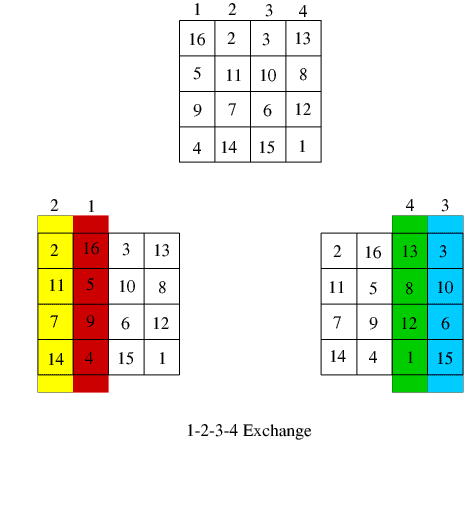
Property 5, the 1-2-3-4 exchange, where the columns 1 and 2 are interchanged as are 3 and 4, is illustrated below. This transformation may also be done by a similar interchange of rows.

 

 

The last transformation produces 3 squares and when used with the other transformations should give 108 different squares. This last number of different squares leaves us far short of the 880 squares of order four enumerated by Frenicle de Bessy in the seventeenth century and illustrated in the book: Berlekamp, E.R.; Conway, J.H. and Guy, R.K. "Winning Ways for Your Mathematical Plays, Vol. 2: Games in Particular'', London Academic Press, 1982. (pp.778-783). Perhaps it is possible to transform the squares alternately by property 3, then 4, 3 again, etc. and produce different magic squares? However, 880 different squares all from one square transformed is rather a tall order. Perhaps there exists a different square that can not be transformed from the others? To look at this last possibility, let's consider different methods of forming a 4 by 4 magic square.

One such method of construction of squares is the "Doubly Even'' method for order $n=4m$, where $m\geq 1$. When $m=1$, we have $n=4$: the size of square we are studying. This method replaces each entry, $a_{i j}$, of a consecutively numbered square's diagonal by $(n^2+1)-a_{i j}$, or equivalently, reverses the order of the diagonal entries.

 

But reversing the order of the diagonal entries would yield the same result as the paired exchange method used in the first article on magic squares. See below and compare the results with the 4 by 4 square in the figure in the next section.

 

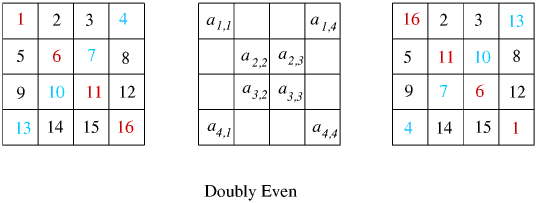
Another choice of construction is allowed with the "exchanged pair method'' as described in the article "Magic Squares" . Using this method we exchanged pairs on the diagonals which gives the same results as was already stated. The paired exchange method is shown again below.

 

 

However, we could have made a different choice of numbers to exchange. With the 4 by 4 square, the 2 and the 14 exchanged and the 3 and the 15 exchanged would balance the 1^st and the 4^th rows. Likewise, the 1^st and 4^th columns would be balanced if the 5 and the 8 were exchanged and the 9 and the 12 were exchanged. Then exchanging the 6 and 11 and the 7 and 10 balances the 2^nd and 3^rd rows and columns. The result is shown below and looks like a different magic square.

 

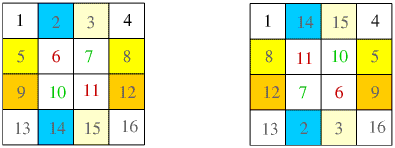
Unfortunately, if this last magic square is rotated by $180^{\circ}$ we have the Durer "Melancholia'' magic square which was a transformation of the original paired exchange method. So, no new magic squares yet.

Perhaps you can find some 4 by 4 magic squares which are not transformations of the above squares? Do any transformations or combination of transformations lead to the same magic square? Are there any other transformations I have not mentioned?