Copyright © University of Cambridge. All rights reserved.
'8 Methods for Three by One' printed from https://nrich.maths.org/
Show menu
Update: Nov 2012: A new pure geometry method was sent in by Sigi. You can see Sigi's method here.
Sigi suggests that certain solutions are dependent in that they use different notations for the same underlying contexts. Sigi suggests the following interesting task: Which of the different methods are genuinely mathematically independent of each other? Certainly something to think about.
Consider the problem is as follows: for the following diagram, prove that $a+b=c $
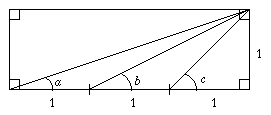
This problem has been shown on NRICH before. When first shown on NRICH it was solved in 8 different ways by a pair of students Alex and Neil. When we again showed the problem, Sigi sent us a lovely geometric proof.
Once you have gone as far as you can with this, try to follow some of Alex's and Neil's solutions for the parts of mathematics with which you are most familiar:
Sigi's proof is three-by-one.pdf . The distinct proofs from Alex and Neil are:
Method 1: Tan Angle Sum Formula
Method 2: Sin Angle Sum Formula
Method 3: Cosine Rule
Method 4: Vector
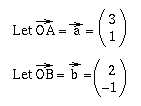
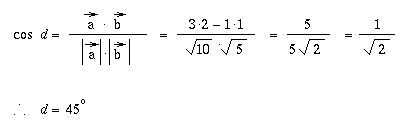
Hence the result is proved.
Method 5: Matrices
Method 6: Pure Geometry
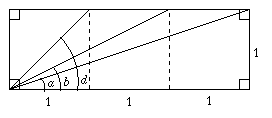
By looking at the leftmost unit square this diagram can be drawn
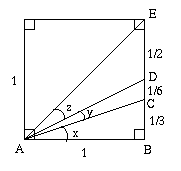
$a+b=c \Leftrightarrow x+x+y = x+y+z \Leftrightarrow x=z$
Hence it must be proven than $x=z$:
Split triangle ADE into two right angled triangles ADF and EDF
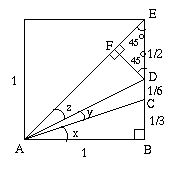
From this it can be seen that
$$
EF = DF = \frac{\sqrt{2}}{4}
$$
and
$$
AF = AE-FE = \sqrt{2} -\frac{\sqrt{2}}{4} = \frac{3\sqrt{2}}{4}
$$
Thus
$$
AF:AB = \frac{3\sqrt{2}}{4}:1
$$
and
$$
DF:BC = \frac{\sqrt{2}}{4}:\frac{1}{3} = \frac{3\sqrt{2}}{4}:1
$$
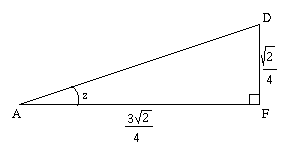
Hence ADF and ABC are similar triangles and, therefore, $x=z$. Thus, $a+b=c$.
Method 7: Coordinate Geometry
Method 8: Complex Numbers
Sigi suggests that certain solutions are dependent in that they use different notations for the same underlying contexts. Sigi suggests the following interesting task: Which of the different methods are genuinely mathematically independent of each other? Certainly something to think about.
Consider the problem is as follows: for the following diagram, prove that $a+b=c $

This problem has been shown on NRICH before. When first shown on NRICH it was solved in 8 different ways by a pair of students Alex and Neil. When we again showed the problem, Sigi sent us a lovely geometric proof.
Once you have gone as far as you can with this, try to follow some of Alex's and Neil's solutions for the parts of mathematics with which you are most familiar:
Sigi's proof is three-by-one.pdf . The distinct proofs from Alex and Neil are:
Method 1: Tan Angle Sum Formula
Proof
From the diagram, $a =\tan^{-1}(1/3), b =\tan^{-1}(1/2)$, and $c = \tan^{-1}(1)$.
We have to prove $a+b=c$, which is the same as proving that $\tan^{-1}(1/3)+\tan^{-1}(1/2)=\tan^{-1}(1)$.
Note that
$$
\begin{eqnarray}
\tan\left(\tan^{-1}\left(\frac{1}{3}\right)+\tan^{-1}\left(\frac{1}{2}\right)\right)
&=&\frac{\tan\left(\tan^{-1}\left(\frac{1}{3}\right)\right)+\tan\left(\tan^{-1}\left(\frac{1}{2}\right)\right)}
{1-\tan\left(\tan^{-1}\left(\frac{1}{3}\right)\right)\tan\left(\tan^{-1}\left(\frac{1}{2}\right)\right)}\cr &=&\frac{\frac{1}{3}+\frac{1}{2}}{1-\frac{1}{3}\cdot\frac{1}{2}}\cr &=&1
\end{eqnarray}
$$
From the diagram, $a =\tan^{-1}(1/3), b =\tan^{-1}(1/2)$, and $c = \tan^{-1}(1)$.
We have to prove $a+b=c$, which is the same as proving that $\tan^{-1}(1/3)+\tan^{-1}(1/2)=\tan^{-1}(1)$.
Note that
$$
\begin{eqnarray}
\tan\left(\tan^{-1}\left(\frac{1}{3}\right)+\tan^{-1}\left(\frac{1}{2}\right)\right)
&=&\frac{\tan\left(\tan^{-1}\left(\frac{1}{3}\right)\right)+\tan\left(\tan^{-1}\left(\frac{1}{2}\right)\right)}
{1-\tan\left(\tan^{-1}\left(\frac{1}{3}\right)\right)\tan\left(\tan^{-1}\left(\frac{1}{2}\right)\right)}\cr &=&\frac{\frac{1}{3}+\frac{1}{2}}{1-\frac{1}{3}\cdot\frac{1}{2}}\cr &=&1
\end{eqnarray}
$$
Method 2: Sin Angle Sum Formula
Proof
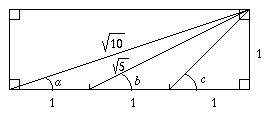
Using Pythagoras we can calculate the lengths of the diagonal lines:
$$
\sin a = \frac{1}{\sqrt{10}}\quad \cos a = \frac{3}{\sqrt{10}}\quad \sin c = \frac{1}{\sqrt{2}}\quad \sin b = \frac{1}{\sqrt{5}}\quad \cos b = \frac{2}{\sqrt{5}}
$$
Using the identity $\sin(a+b) = \sin a \cos b + \sin b \cos a$ we see that
$$
\begin{eqnarray}
\sin(a+b) &=& \frac{1}{\sqrt{10}}\cdot\frac{2}{\sqrt{5}}+\frac{1}{\sqrt{5}}\cdot \frac{3}{\sqrt{10}}\cr
&=& \frac{2+3}{\sqrt{10\cdot 5}}\cr
&=& \frac{5}{\sqrt{50}}\cr
&=&\frac{1}{\sqrt{2}}\cr
&=& \sin c
\end{eqnarray}
$$
Hence the result is proved.
Using Pythagoras we can calculate the lengths of the diagonal lines:

$$
\sin a = \frac{1}{\sqrt{10}}\quad \cos a = \frac{3}{\sqrt{10}}\quad \sin c = \frac{1}{\sqrt{2}}\quad \sin b = \frac{1}{\sqrt{5}}\quad \cos b = \frac{2}{\sqrt{5}}
$$
Using the identity $\sin(a+b) = \sin a \cos b + \sin b \cos a$ we see that
$$
\begin{eqnarray}
\sin(a+b) &=& \frac{1}{\sqrt{10}}\cdot\frac{2}{\sqrt{5}}+\frac{1}{\sqrt{5}}\cdot \frac{3}{\sqrt{10}}\cr
&=& \frac{2+3}{\sqrt{10\cdot 5}}\cr
&=& \frac{5}{\sqrt{50}}\cr
&=&\frac{1}{\sqrt{2}}\cr
&=& \sin c
\end{eqnarray}
$$
Hence the result is proved.
Method 3: Cosine Rule
This method required us to extend the diagram as follows:
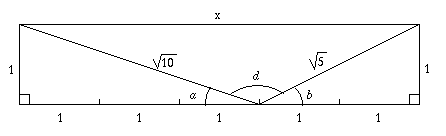
From the altered diagram it can be seen that $x=3+2=5$.
Next, $d$ can be found using the cosine rule $c^2= a^2+b^2-2ab \cos C$.
Substitution of these values gives
$$
\cos d = \frac{-1}{\sqrt{2}}
$$
Thus $d=135^\circ$. Therefore $a+b = 180^\circ - d = 45^\circ = c$
Hence the result is proved.

From the altered diagram it can be seen that $x=3+2=5$.
Next, $d$ can be found using the cosine rule $c^2= a^2+b^2-2ab \cos C$.
Substitution of these values gives
$$
\cos d = \frac{-1}{\sqrt{2}}
$$
Thus $d=135^\circ$. Therefore $a+b = 180^\circ - d = 45^\circ = c$
Hence the result is proved.
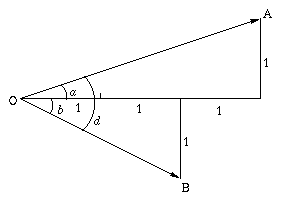
Method 4: Vector

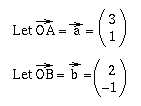
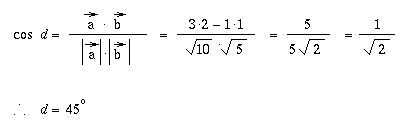
Hence the result is proved.
Method 5: Matrices
Let $\bf{d} = (x, y)$ be any point in the $x-y$ plane. Let $\bf{d}_1$ be the point obtained by rotating $a^\circ$ about the origin.
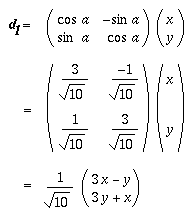
Let $\bf{d}_2$ be the point obtained by rotating $\bf{d}_1$ by $b^\circ$ around the origin.
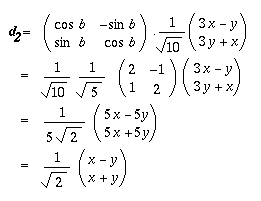
Finally, let $\bf{d}_2$ be the point obtained by rotating $\bf{d}$ by $c^\circ$ around the origin.
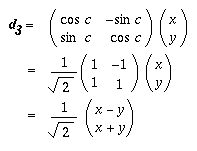
Hence a rotation by $a+b$ is the same as a rotation by $c$ degrees. Hence, $a+b=c$, as none of the angles is greater than $90^\circ$.
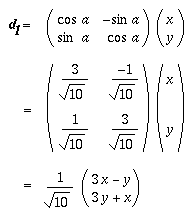
Let $\bf{d}_2$ be the point obtained by rotating $\bf{d}_1$ by $b^\circ$ around the origin.
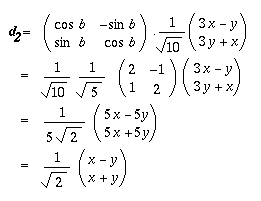
Finally, let $\bf{d}_2$ be the point obtained by rotating $\bf{d}$ by $c^\circ$ around the origin.
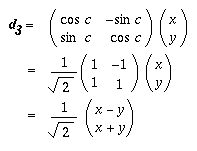
Hence a rotation by $a+b$ is the same as a rotation by $c$ degrees. Hence, $a+b=c$, as none of the angles is greater than $90^\circ$.
Method 6: Pure Geometry

By looking at the leftmost unit square this diagram can be drawn

$a+b=c \Leftrightarrow x+x+y = x+y+z \Leftrightarrow x=z$
Hence it must be proven than $x=z$:
Split triangle ADE into two right angled triangles ADF and EDF

From this it can be seen that
$$
EF = DF = \frac{\sqrt{2}}{4}
$$
and
$$
AF = AE-FE = \sqrt{2} -\frac{\sqrt{2}}{4} = \frac{3\sqrt{2}}{4}
$$
Thus
$$
AF:AB = \frac{3\sqrt{2}}{4}:1
$$
and
$$
DF:BC = \frac{\sqrt{2}}{4}:\frac{1}{3} = \frac{3\sqrt{2}}{4}:1
$$
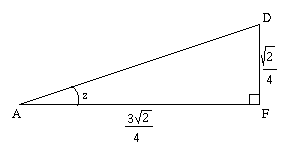
Hence ADF and ABC are similar triangles and, therefore, $x=z$. Thus, $a+b=c$.
Method 7: Coordinate Geometry
The coordinate geometry proof is based on the following diagram; the gradients are easy to read off the original image.
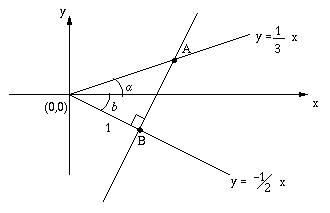
Let $B$ be the point $( x_B ,y_B )$ on the line $y = -\frac{1}{2} x$ at a distance of $1$ from the origin. Since $\sqrt{x^2_B+y^2_B} = 1$ and $y_B = -\frac{1}{2}x_B$ we have
$$
\begin{eqnarray}
\sqrt{x^2_B+\frac{1}{4}x^2_B} &=& \sqrt{\frac{5}{4}x^2_B} = 1\cr
\Rightarrow x_B = \frac{2}{\sqrt{5}}\cr
\Leftrightarrow y_B = \frac{-1}{\sqrt{5}}
\end{eqnarray}
$$
Thus,
$$
B=\left(\frac{2}{\sqrt{5}}, \frac{-1}{\sqrt{5}}\right)
$$
We can now determine the equation of the line through $B$ perpendicular to the line $y = -\frac{1}{2} x$ to be
$$
y = 2x-\sqrt{5}.
$$
This line intersects $y=\frac{1}{3} x$ at $A$ which we can calculate to be
$$
A= \left(\frac{3}{\sqrt{5}}, \frac{1}{\sqrt{5}}\right)
$$
Now that we konw points $A$ and $B$ we can calculate the distance between them as
$$
|AB| = \sqrt{\left(\frac{3}{\sqrt{5}}-\frac{2}{\sqrt{5}}\right)^2 +\left(\frac{1}{\sqrt{5}}+\frac{1}{\sqrt{5}}\right)^2}= \sqrt{\frac{1}{5}+\frac{4}{5}}=1
$$
Referring back to the diagram shows that $a+b=45^\circ$ and the result is proved.

Let $B$ be the point $( x_B ,y_B )$ on the line $y = -\frac{1}{2} x$ at a distance of $1$ from the origin. Since $\sqrt{x^2_B+y^2_B} = 1$ and $y_B = -\frac{1}{2}x_B$ we have
$$
\begin{eqnarray}
\sqrt{x^2_B+\frac{1}{4}x^2_B} &=& \sqrt{\frac{5}{4}x^2_B} = 1\cr
\Rightarrow x_B = \frac{2}{\sqrt{5}}\cr
\Leftrightarrow y_B = \frac{-1}{\sqrt{5}}
\end{eqnarray}
$$
Thus,
$$
B=\left(\frac{2}{\sqrt{5}}, \frac{-1}{\sqrt{5}}\right)
$$
We can now determine the equation of the line through $B$ perpendicular to the line $y = -\frac{1}{2} x$ to be
$$
y = 2x-\sqrt{5}.
$$
This line intersects $y=\frac{1}{3} x$ at $A$ which we can calculate to be
$$
A= \left(\frac{3}{\sqrt{5}}, \frac{1}{\sqrt{5}}\right)
$$
Now that we konw points $A$ and $B$ we can calculate the distance between them as
$$
|AB| = \sqrt{\left(\frac{3}{\sqrt{5}}-\frac{2}{\sqrt{5}}\right)^2 +\left(\frac{1}{\sqrt{5}}+\frac{1}{\sqrt{5}}\right)^2}= \sqrt{\frac{1}{5}+\frac{4}{5}}=1
$$
Referring back to the diagram shows that $a+b=45^\circ$ and the result is proved.
Method 8: Complex Numbers
This method uses aspects of other proofs presented (and therefore could be shortened) but we include it because it gives a nice example of how complex numbers, matrices and all other methods fit nicely together.
Let $r=\sqrt{x^2+y^2}$.
Now, the complex number corresponding to the point with coordinates $(x, y)$ in the argand diagram can be written as
$$
z= x+iy = r\exp\left(i\tan^{-1} \left(\frac{y}{x}\right)\right)
$$
Let $z'$ be the complex number obtained by rotating $z$ by $2(a+b)$ degrees. Then we can use the identities $\sin(a+b) = \sin a \cos b +\cos a\sin b$ and $\cos(a+b) = \cos a \cos b-\sin a \sin b$ to see that:
$$
\begin{eqnarray}
z' &=& r\exp\left(i\tan^{-1}\left(\frac{y}{x}\right)+2i(a+b)\right)\cr
&=& r\left[\cos\left(\tan^{-1}\left(\frac{y}{x}\right)+2(a+b)\right)+i\sin\left(\tan^{-1}\left(\frac{y}{x}\right)+2(a+b)\right)\right]\cr
&=&r\left[\cos\left(\tan^{-1}\left(\frac{y}{x}\right)\right)\cos\left(2(a+b)\right)-\sin\left(\tan^{-1}\left(\frac{y}{x}\right)\right)\sin\left(2(a+b)\right)\right]\cr
&& +ir\left[ \sin\left(\tan^{-1}\left(\frac{y}{x}\right)\right)\cos\left(2(a+b)\right)+\cos\left(\tan^{-1}\left(\frac{y}{x}\right)\right)\sin\left(2(a+b)\right) \right]
\end{eqnarray}
$$
We can simplify the arctangents by considering the following diagram:
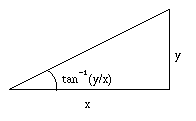
From this we can see that $\cos\left(\tan^{-1}\left(\frac{y}{x}\right) \right)= \frac{x}{r}$ and $\sin\left(\tan^{-1}\left(\frac{y}{x}\right) \right)= \frac{y}{r}$
This simplifies the expression for $z'$ to
$$
z' = x\cos\left(2(a+b)\right)-y\sin\left(2(a+b)\right)+i\left(y\cos\left(2(a+b)\right)+x\sin\left(2(a+b)\right)\right)
$$
Alex and Neil then used some double angle formulae and the fact that $\sin(a+b)=\cos(a+b)=\frac{1}{\sqrt{2}}$ to determine that
$$
z' = -y+ix
$$
Since this is a complex number rotated through $90^\circ$ we can conclude that $a+b = 45^\circ$
Let $r=\sqrt{x^2+y^2}$.
Now, the complex number corresponding to the point with coordinates $(x, y)$ in the argand diagram can be written as
$$
z= x+iy = r\exp\left(i\tan^{-1} \left(\frac{y}{x}\right)\right)
$$
Let $z'$ be the complex number obtained by rotating $z$ by $2(a+b)$ degrees. Then we can use the identities $\sin(a+b) = \sin a \cos b +\cos a\sin b$ and $\cos(a+b) = \cos a \cos b-\sin a \sin b$ to see that:
$$
\begin{eqnarray}
z' &=& r\exp\left(i\tan^{-1}\left(\frac{y}{x}\right)+2i(a+b)\right)\cr
&=& r\left[\cos\left(\tan^{-1}\left(\frac{y}{x}\right)+2(a+b)\right)+i\sin\left(\tan^{-1}\left(\frac{y}{x}\right)+2(a+b)\right)\right]\cr
&=&r\left[\cos\left(\tan^{-1}\left(\frac{y}{x}\right)\right)\cos\left(2(a+b)\right)-\sin\left(\tan^{-1}\left(\frac{y}{x}\right)\right)\sin\left(2(a+b)\right)\right]\cr
&& +ir\left[ \sin\left(\tan^{-1}\left(\frac{y}{x}\right)\right)\cos\left(2(a+b)\right)+\cos\left(\tan^{-1}\left(\frac{y}{x}\right)\right)\sin\left(2(a+b)\right) \right]
\end{eqnarray}
$$
We can simplify the arctangents by considering the following diagram:
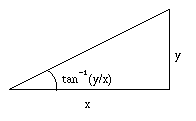
From this we can see that $\cos\left(\tan^{-1}\left(\frac{y}{x}\right) \right)= \frac{x}{r}$ and $\sin\left(\tan^{-1}\left(\frac{y}{x}\right) \right)= \frac{y}{r}$
This simplifies the expression for $z'$ to
$$
z' = x\cos\left(2(a+b)\right)-y\sin\left(2(a+b)\right)+i\left(y\cos\left(2(a+b)\right)+x\sin\left(2(a+b)\right)\right)
$$
Alex and Neil then used some double angle formulae and the fact that $\sin(a+b)=\cos(a+b)=\frac{1}{\sqrt{2}}$ to determine that
$$
z' = -y+ix
$$
Since this is a complex number rotated through $90^\circ$ we can conclude that $a+b = 45^\circ$