Somewhat surprisingly every Pythagorean triple $( a, b, c)$, where $a, b$ and $c$ are positive integers and $a^2+b^2 = c^2$, can be illustrated by this diagram, in which the L shaped region has area $b^2$, and the areas of the larger and smaller squares are $c^2$ and $a^2$. With this clue you can find some triples for yourself right away. With an L strip of width 1 unit you get the whole class of Pythagorean triples with $a$ and $c$ as consecutive integers, that is $c = a+1.$

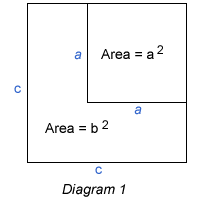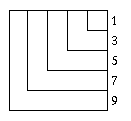Diagram 2

This diagram (extended as far as required) illustrates the fact that, for all $n$, the sum of the first $n$ odd numbers gives $n^2$. As we can see from the diagram to the left: \begin{eqnarray}1+3&=&2^2&=&4 \\ 1+3+5 &=& 3^2 &=& 9 \\ 1+3 +5 + 7 &=& 4^2 &=& 16 \\ 1+3+5+7+9 &=& 5^2 &=& 25 \end{eqnarray}

To find other triples with L strips of different widths try this for yourself: choose any two positive integers $p$ and $q$ that have no common factors and with $p > q$; \item calculate $2p q$ and $p^2+q^2$; \item draw two squares with sides $a=2p q$ and $c = p^2 + q^2$ as shown in Diagram 3. The width of the L strip is $w = (p-q)^2$ and its area is $b^2 = (p^2 -q^2)^2$, and if you wish you can check this algebra for yourself. 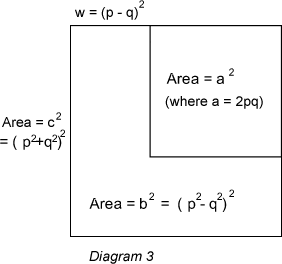For example, taking $p= 5$ and $q= 2$, the inner square has dimensions $20$ by $20$ and the outer square has dimensions $29$ by $29$, the width of the L strip is $9$, and the area of the L strip is $(25-4)^2=21^2$, giving the Pythagorean triple $(20, 21, 29)$.

We shall concentrate on finding all the triples where $a, b$ and $c$ have no common factor. If $p$ and $q$ have a common factor, or if $p$ and $q$ are both odd, then $a, b$ and $c$ will have a common factor.

We only need the cases where one of $p$ and $q$ is even and the other is odd. In such cases the width of the L strip $= c-a=(p-q)^2$ is always an odd square.

The table below (extended in the obvious way) shows all the `primitive' Pythagorean triples, and some non-primitive triples as well.

Pythagorean Triples	$c-b=1^2$ ($p=q+1$)	$c-b=3^2$ ($p=q+3$)	$c-b=5^2$ ($p=q+5$)	$c-b=7^2$ ($p=q+7$)	$c-b=9^2$ ($p=q+9$)
$c-a=2 \times 1^2$ $(q=1)$	3, 4, 5	15, 8, 17	35, 12, 37	63, 16, 65	99, 20, 101
$c-a=2 \times 2^2$ $(q=2)$	5, 12, 13	21, 20, 29	45, 28, 53	77, 36, 85	117, 44, 125
$c-a=2 \times 3^2$ $ (q=3)$	7, 24, 25	27, 36, 45	55, 48, 73	91, 60, 109	135, 72, 153
$c-a=2 \times 4^2$ $(q=4)$	9, 40, 41	33, 56, 65	65, 72, 97	105, 88, 137	153, 104, 185
$c-a=2 \times 5^2$ $(q=5)$	11, 60, 61	39, 80, 89	75, 100, 125	119, 120, 169	171, 140, 221
$c-a=2 \times 6^2$ $(q=6)$	13, 84, 85	45, 108, 117	85, 132, 157	133, 156, 205	189, 180, 261
$c-a=2 \times 7^2$ $ (q=7)$	15, 112, 113	51, 140, 149	95, 168, 193	147, 196, 245	207, 224, 305
$c-a=2 \times 8^2$ $(q=8)$	17, 144, 145	57, 176, 185	105, 208, 233	161, 240, 289	225, 272, 353
$c-a=2 \times 9^2$ $(q=9)$	19, 180, 181	63, 216, 225	115, 252, 277	175, 288, 337	243, 324, 405

There is a dual illustration of each triple where the smaller square has side $p^2 - q^2$ and the width of the L strip is $2q^2$. In the dual case for $p=5$ and $q =2$ the inner square has dimensions $21$ by $21$ and the width of the L strip is $8$ units giving the triple $(20,21,29)$.

Given a Pythagorean triple $(a, b, c)$ you can always `work back' to find $p$ and $q$, and given $p$ and $q$ you can always calculate $a, b$ and $c$. You could compete with a friend, both choose a value for $p$ and $q$ and compute a Pythagorean triple $(a, b, c)$ which you give to the other person. Then without using calculators, see who can be the first to find the values of $p$ and $q$. You may need to keep $p$ and $q$ small at first to make this easy for yourselves but as you get better you can take bigger values of $p$ and $q$.