Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Age 14 to 18
Published 1998 Revised 2009
Picturing Pythagorean Triples
Somewhat surprisingly every Pythagorean triple $( a, b, c)$,
where $a, b$ and $c$ are positive integers and $a^2+b^2 = c^2$, can
be illustrated by this diagram, in which the L shaped region has
area $b^2$, and the areas of the larger and smaller squares are
$c^2$ and $a^2$.
With this clue you can find some triples for yourself right
away. With an L strip of width 1 unit you get the whole class of
Pythagorean triples with $a$ and $c$ as consecutive integers, that
is $c = a+1.$
|
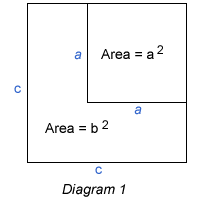 |
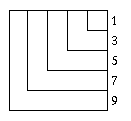 Diagram 2
|
This diagram (extended as far as required)
illustrates the fact that, for all $n$, the sum of the first $n$
odd numbers gives $n^2$. As we can see from the diagram to the
left:
\begin{eqnarray}1+3&=&2^2&=&4 \\ 1+3+5 &=&
3^2 &=& 9 \\ 1+3 +5 + 7 &=& 4^2 &=& 16 \\
1+3+5+7+9 &=& 5^2 &=& 25 \end{eqnarray}
|
Taking $a= 4$ and $c= 5$, the area of the outer ``L'' strip is
$b^2= 9$ and this gives the first Pythagorean triple $4^2+ 3^2=
5^2$.
Before reading on, can you use more strips of unit width and
extend the diagram to find Pythagorean triples with $b^2 = 25, 49,
81, 121$ etc.?
For every odd square number $b^2$, we can pick out a
Pythagorean triple.
As the Diagram 2 shows, $c = a + 1$ and hence \begin{eqnarray}
b^2 = c^2 - a^2 \\ b^2 = (a+1)^2 - a^2 \\ b^2 = a^2 + 2a +1 -a^2\\
= 2a + 1 \end{eqnarray} The next odd square after $3^2 = 9$ is $5^2
= 25$
Let $$25 = b^2$$
$$25 = 2*12 + 1$$
giving $a$ = 12 and from there the triple
$5^2+12^2=13^2$
The next one in this class is $b=7$ giving $a=24 =
\frac{(49-1)}{2}$ and $c=25$
Giving the triple $24^2+7^2=25^2$, and so on.
This method gives us infinitely many Pythagorean triples, but
what about others where the width of the L strip (the difference
between $a$ and $c$) is more than 1?
 |
To find other triples with L strips of different widths try
this for yourself:
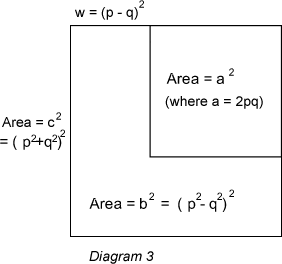
For example, taking $p= 5$ and $q= 2$, the inner square has
dimensions $20$ by $20$ and the outer square has dimensions $29$ by
$29$, the width of the L strip is $9$, and the area of the L strip
is $(25-4)^2=21^2$, giving the Pythagorean triple $(20, 21,
29)$.
|
The process given by these instructions produces what is
called a parameterisation and $p$ and $q$ are called parameters. It
is easy to show by simple algebra that, by choosing positive
integers $p$ and $q$, with $p> q$, and taking
$$b = p^2-q^2$$
$$a = 2p q$$
$$c = p^2 + q^2$$
we get a Pythagorean triple.
This does not give all triples, for example it does not give
($9,12,15)$, but it does give all triples for which $a, b$ and $c$
have no common factor (`primitive' triples). Every other triple can
then be found by calculating $( k a, k b, k c)$ for some integer
$k$.
These results are proved in the article Pythagorean
Triples II .
We shall concentrate on finding all the triples where $a, b$ and $c$ have no common factor. If $p$ and $q$ have a common factor, or if $p$ and $q$ are both odd, then $a, b$ and $c$ will have a common factor.
We only need the cases where one of $p$ and $q$ is even and the other is odd. In such cases the width of the L strip $= c-a=(p-q)^2$ is always an odd square.
The table below (extended in the obvious way) shows all the `primitive' Pythagorean triples, and some non-primitive triples as well.
| Pythagorean Triples | $c-b=1^2$ ($p=q+1$) |
$c-b=3^2$ ($p=q+3$) |
$c-b=5^2$ ($p=q+5$) |
$c-b=7^2$ ($p=q+7$) |
$c-b=9^2$ ($p=q+9$) |
|---|---|---|---|---|---|
|
$c-a=2 \times 1^2$
$(q=1)$
|
3, 4, 5 | 15, 8, 17 | 35, 12, 37 | 63, 16, 65 |
99, 20, 101
|
|
$c-a=2 \times 2^2$
$(q=2)$
|
5, 12, 13 | 21, 20, 29 | 45, 28, 53 | 77, 36, 85 | 117, 44, 125 |
|
$c-a=2 \times 3^2$
$ (q=3)$
|
7, 24, 25 | 27, 36, 45 | 55, 48, 73 | 91, 60, 109 | 135, 72, 153 |
|
$c-a=2 \times 4^2$
$(q=4)$
|
9, 40, 41 | 33, 56, 65 | 65, 72, 97 | 105, 88, 137 | 153, 104, 185 |
|
$c-a=2 \times 5^2$
$(q=5)$
|
11, 60, 61 | 39, 80, 89 | 75, 100, 125 | 119, 120, 169 | 171, 140, 221 |
|
$c-a=2 \times 6^2$
$(q=6)$
|
13, 84, 85 | 45, 108, 117 | 85, 132, 157 | 133, 156, 205 | 189, 180, 261 |
|
$c-a=2 \times 7^2$
$ (q=7)$
|
15, 112, 113 | 51, 140, 149 | 95, 168, 193 | 147, 196, 245 | 207, 224, 305 |
|
$c-a=2 \times 8^2$
$(q=8)$
|
17, 144, 145 | 57, 176, 185 | 105, 208, 233 | 161, 240, 289 | 225, 272, 353 |
|
$c-a=2 \times 9^2$
$(q=9)$
|
19, 180, 181 | 63, 216, 225 | 115, 252, 277 | 175, 288, 337 | 243, 324, 405 |
There is a dual illustration of each triple where the smaller square has side $p^2 - q^2$ and the width of the L strip is $2q^2$. In the dual case for $p=5$ and $q =2$ the inner square has dimensions $21$ by $21$ and the width of the L strip is $8$ units giving the triple $(20,21,29)$.
Given a Pythagorean triple $(a, b, c)$ you can always `work back' to find $p$ and $q$, and given $p$ and $q$ you can always calculate $a, b$ and $c$. You could compete with a friend, both choose a value for $p$ and $q$ and compute a Pythagorean triple $(a, b, c)$ which you give to the other person. Then without using calculators, see who can be the first to find the values of $p$ and $q$. You may need to keep $p$ and $q$ small at first to make this easy for yourselves but as you get better you can take bigger values of $p$ and $q$.