These simple puzzles have been selected because they require no knowledge of knot theory, just a careful inspection of the patterns. The puzzles are taken from The Knots Puzzle Book by Heather McLeay published by Tarquin Publications [1] . The book gives a simple introduction to the classification of knots and a little about prime knots, crossing numbers and knot arithmetic, just enough theory for solving some more puzzles. 

A mathematical knot is really an "endless knot'' made from a single strand, with crossovers where one piece of the rope crosses another piece, and the ends joined together to make it continuous. The rope can then be rearranged, but not untied, and however it is handled the knot remains essentially the same. Knots which can be rearranged to have no crossovers at all are called unknots.

The best way to start a study of knots is by actually tying them which you may find easier than drawing. Knots constructed from linked strands are referred to as "links'' and colouring the separate strands, or tying the knots with different coloured ropes, will help you to investigate the different types.

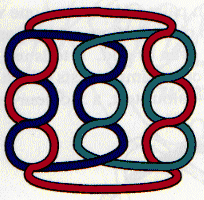
Some of these decorative knot patterns are formed from a single strand, others from several strands. How many separate strands are needed to make up each of these designs?

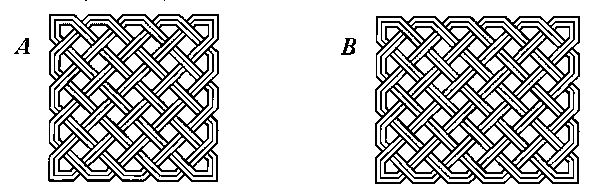
The two Celtic knot patterns below look very similar except that one might be described as a 'four by four' and the other as a 'five by four'. What is the fundamental difference between them? Some patterns like this can be formed from a single strand and others need several strands, what can you say about the dimensions of these two types?

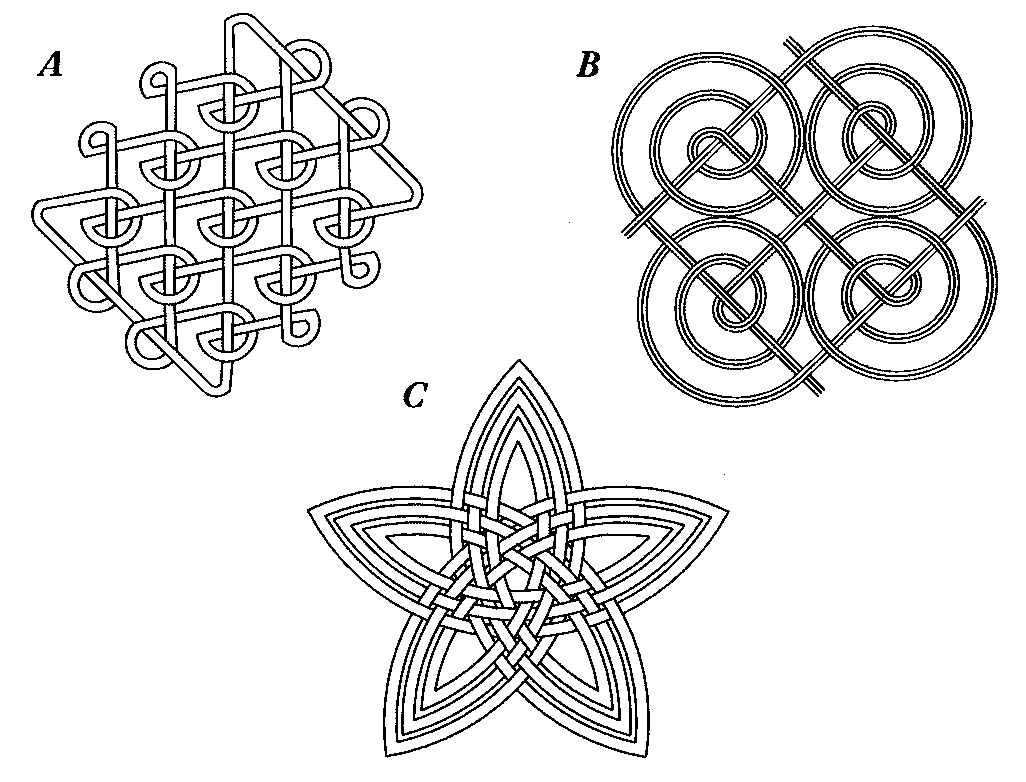
Which of these diagrams show knots made from single strands and which are made from linked strands?

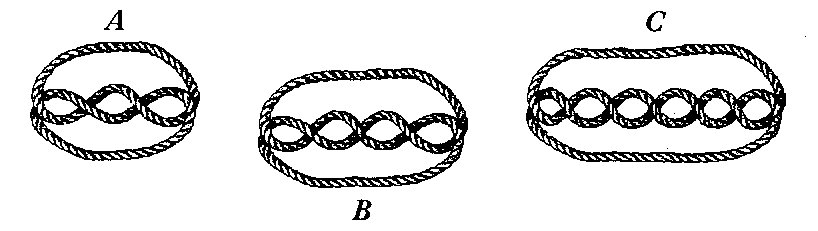
How many linked strands do you need to make a ten crossing version of the diagram above?

Here are some examples of more complicated links. How many separate strands are there in each case?

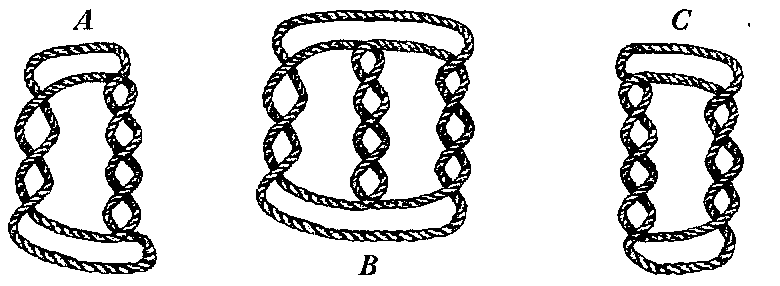
Is there an easy way to predict how many strands knots like these will have?

In his article entitled Celtic Design, in the March 1998 issue of Mathematics in School [2], John Matthews describes how he used the !DRAW package on an Acorn 310 to design five basic squares and then to 'grid lock', 'copy' and 'transform' the squares, assembling the copies to produce Celtic patterns and to design his own. You might like to try this for yourself. In the same article John produces sets of tiles, with just the right number of each of the five basic squares in the set, so that the tiles can be fitted together, like a jigsaw, to make a given design. The article gives sets of tiles for five designs. With this idea you can easily produce lots of the tiles and make up your own designs. Here we are at the borders of mathematics, art and design! Thank you John for a delightful starter to many more knotty possibilities.
 

[1] Address for Tarquin Publications: Stradbroke, Diss, Norfolk IP21 5JP, England.
[2] For further information you can write to John Matthews, Auchenharvie Academy, Saltoats Rd, Stevenston, Scotland, KA20 3JW.