Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Age 16 to 18
Published 1998 Revised 2008
The Dodecahedron Explained
What is the shortest distance through the centre of a regular dodecahedron between the centres of opposite faces? This problem first appeared in November 1997 and the solution to the alternative problem for the shortest route on the surface of the dodecahedron was published in December. Well done Luke both for the mathematical work and for the quality of your exposition. We hope this will inspire other students.
Let $O$ be the centre of 3 spheres: the circumsphere (through the vertices), the midsphere (through the midpoints of the edges) and the insphere (which touches the faces at their centres). These have radii $r_0$, $r_1$ and $r_2$ respectively. Hence our problem is to find $2r_2$. Let the side length of the dodecahedron be 1 unit.
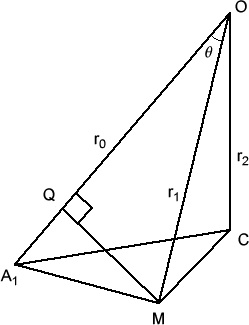
Consider a face with vertices $A_1$, $A_2$, $\ldots$, $A_5$.
Let $M$ be the midpoint of $A_1 A_2$ and the centre of this face be
$C$. Let $Q$ be the foot of the perpendicular from $M$ onto $A_1
O$. Now $A_1 O=r_0$, $O M=r_1$, $O C=r_2$.
Note that
- $\angle A_1 M C=\frac{\pi}{2}$ ($A_1 A_2 C$ isosceles; $M$ is midpoint of base $A_1 A_2$),
- $\angle O C M=\frac{\pi}{2}$ (sphere centre $O$, radius $O C$ touches plane $A_1 M C$ at $C$), and
- $\angle A_1 M O=\frac{\pi}{2}$ ($O M$ is altitude of triangle $A_1 O A_2$).
Also, $\angle A_1 C M=\frac{\pi}{5}$ by considering angles at
the centre $C$ of the pentagon $A_1 A_2 A_3 A_4 A_5$.
Let $A_1 O M=\theta$.
We consider the triangle formed by the midpoints of the 3
edges from $A_1$ (let these be $L$, $M$, $N$, with $M$ the midpoint
of $A_1 A_2$) and the quadrilateral $C M A_1 N$:
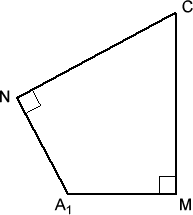
These points are concyclic, so $\angle N A_1 M=\pi - \angle N C M =\pi-\frac{2\pi}{5}$ (by considering angles at the centre of $A_1 A_2 A_3 A_4 A_5$).
In isosceles triangle $A_1 M N$, $$ \angle A_1 N M=\frac{1}{2}(\pi-\angle N A_1 M)=\frac{\pi}{5}. $$ By the sine rule, $$ \frac{A_1 M}{\sin\frac{\pi}{5}}=\frac{M N}{\sin\left( \pi-\frac{2\pi}{5}\right)} $$ but $A_1 M=\frac{1}{2}$, i.e., $$ \frac{\sin\frac{2\pi}{5}}{2\sin\frac{\pi}{5}}=M N, $$ therefore \begin{equation} M N =\cos\frac{\pi}{5}. \end{equation} Now clearly plane $L M N$ is perpendicular to $O A_1$, so the centre of triangle $L M N$ is $Q$, foot of the perpendicular from $M$ to $O A_1$. Hence triangle $L M N$ has radius $Q M=\frac{1}{2}\cos\theta$ by simple trig. But from expression 1 and the fact that triangle $L M N$ is equilateral we have that $$ Q M=\frac{1}{\sqrt{3}}\cdot M N=\frac{\cos\frac{\pi}{5}}{\sqrt{3}}. $$ Equating these two expressions, $$ \cos\theta=\frac{2}{\sqrt{3}}\cos\frac{\pi}{5}. $$ Hence \begin{eqnarray} \sin\theta & = & \sqrt{(1-\cos^2\theta)}\\ & = & \sqrt{1-\frac{4}{3}\cos^2\frac{\pi}{5}}\\ & = & \sqrt{\frac{3-4\cos^2\frac{\pi}{5}}{3}}. \end{eqnarray} Now $r_1=\frac{1}{2}\cot\theta$ by simple trig in triangle $O A_1 M$,
and $r_2^2=r_1^2-\left(\frac{1}{2}\cot\frac{\pi}{5}\right)^2$ in triangle $O C M$, so \begin{eqnarray} r_2^2 & = & \frac{cos^2\theta}{4\sin^2\theta}-\frac{\cos^2\frac{\pi}{5}}{4 \sin^2\frac{\pi}{5}}\\ & = & \frac{\frac{4}{3}\cos^2\frac{\pi}{5}}{4\left(\frac{3-4\cos^2 \frac{\pi}{5}}{3}\right)}-\frac{\cos^2\frac{\pi}{5}}{4\sin^2\frac{\pi}{5}}. \end{eqnarray} So \begin{eqnarray} 4r_2^2 & = & 4\cos^2\frac{\pi}{5}\left(\frac{1}{3-4\cos^2\frac{\pi}{5}}- \frac{1}{4\sin^2\frac{\pi}{5}}\right)\\ & = & 4\cos^2\frac{\pi}{5}\left(\frac{4\sin^2\frac{\pi}{5}-3+4\cos^2 \frac{\pi}{5}}{\left(3-4\cos^2\frac{\pi}{5}\right)\left(4\sin^2\frac{\pi} {5}\right)}\right)\\ & = & \frac{\cos^2\frac{\pi}{5}}{\sin^2\frac{\pi}{5}}\cdot\frac{1}{3- 4\cos^2\frac{\pi}{5}}, \end{eqnarray} i.e. $$ 2r_2=\cot\frac{\pi}{5}\sqrt{\frac{1}{3-4\cos^2\frac{\pi}{5}}}. $$ Use $\cos\frac{\pi}{5}=\frac{1+\sqrt{5}}{4}$ to find $2r_2=\cot\frac{\pi}{5}\cdot\frac{1+\sqrt{5}}{2}$,
i.e., the required distance is $$ \left(\cot\frac{\pi}{5}\right)\left(\frac{1+\sqrt{5}}{2}\right) $$ or $$ \sqrt{\frac{11+5\sqrt{5}}{2\sqrt{5}}}\approx 2.23 \; \mathrm{units}. $$