This is the first of two articles writtten for the Summer 1997 NRICH Maths Club Videoconference linking schools in London and Norfolk.

The article poses a number of questions for you to think about. The second article looks at these questions and discusses what you might have discovered.

Einstein's theory of General Relativity brings together geometry and gravity. One of the basic ideas is that an object with mass actually curves the space-time around it. For example, the comet Hale-Bopp followed a path determined by the curvature of space-time produced by the gravitational fields of the sun and other massive bodies.

What do we mean by space-time? Well, imagine making a film of someone walking across a room, then take the actual film, cut it up into the individual frames and stack them (in order!) on top of each other before fusing them together somehow. What you have is a piece of 2+1 = 3-dimensional space-time:

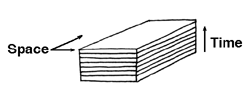2 spatial dimensions in the planes of the photograph. 1 time dimension in the sequence of photographs

We know that time is very different from space in some ways: (e.g. you cannot suddenly decide to go backwards in time!) but Einstein's theory of Special Relativity emphasises the similarities (e.g. the measurement of time, as well as of spatial distance, depends on how the observer is moving).

In these articles on this topic, we shall concentrate on geometry, but we will make contact with gravity at one stage.

In this article we will ask lots of questions for readers to think about and in the second article, "Geometry and Gravity II", we will start to examine some of these questions further.

MATHEMATICAL CONCEPTS

1. CURVATURE

We all have some idea about the difference between flat objects and curved ones. But how can we measure curvature?

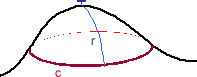
(a) "Gentle" method: to measure the curvature of a surface at a point, place a drawing pin there with a piece of string of length r attached. Keeping the string taut, trace a path on the surface and measure the path's length C.

Question 1: How could you use C to describe the curvature of a surface? How might these relate to ideas of positive and negative curvature?
 

(b) "Brutal" method: press the curved surface down onto a flat surface, making cuts as necessary. There will be gaps and/or overlaps. Try it with egg boxes.

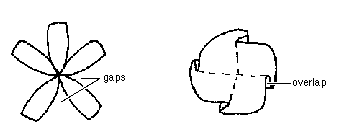
Question 2: How are the gaps and overlaps related to curvature?How might these relate to ideas of positive and negative curvature?

In general this method gives qualitative rather than quantitative information. There is a particular type of surface which is well suited to making measurements of curvature. This is made up of flat triangles (or other polygons) put together in a way which approximates a smoothly curved surface, as in a geodesic dome. Take the triangles meeting at a vertex and flatten them out, after making a cut. In general there will be a gap angle, given by

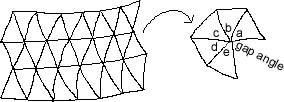
gap angle = 360 degrees - (sum of angles at vertex) = 360 degrees - (a + b + c + d + e ) here

This gap angle is proportional to the curvature at a point. It is large if the surface is very spiky there, and small if the surface is almost flat.

2. GEODESICS

On a flat surface, the shortest distance between two points is a straight line. In general a straight line does not fit on a curved surface but there is something equivalent called a geodesic. It is still the shortest distance between two points along hte surface.

Try stretching a piece of elastic between two points on a globe to find the geodesic (or great circle) between them.

To trace a geodesic on a surface made up of flat triangles, the procedure is as follows:

* within each triangle it is a straight line;

* when it reaches an edge just flatten the surface there and continue the straight line across the edge.

Problems like "The Spider and The Fly" use this idea.

Now try this experiment with geodesics.

* Make a cardboard model of a pyramid (but don't glue it together) and put it in the centre of a flat sheet of paper (you could also use construction pieces such as Polydron for this as they are easier to manipulate)..

* Draw a geodesic approaching the pyramid and follow its course to the other side (you will have to flatten out the pyramid as you do this). Try to avoid vertices by moving your line a bit if necessary.

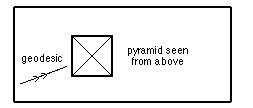
Question 3. Investigate the difference between the initial and final directions of the geodesic in various circumstances:

For example:

* how near to the top vertex the line goes,

* how steep the pyramid is,

* what the angle of approach is etc.

Can you formulate any general rule?

**What situation involving gravity does this model?**

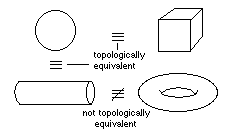
3. TOPOLOGY

Roughly speaking, topology is all about the way objects are put together, their "connectedness". The topology of an object does not change when it is deformed provided no holes are made and no parts stuck together. A ball of plasticene can be distorted into a cube, but that still has the same topology, that of a sphere. A ball can be squeezed into a sausage shape and the ends stuck together - its topology has changed into that of a doughnut (or torus, to give it its technical name).

Question 4: A FINAL PROBLEM BRINGING THESE IDEAS TOGETHER

A. Try to find, construct, draw or just visualise as many "triangulated" closed surfaces as possible:

(i) the 5 regular solids, the tetrahedron, cube, octahedron, dodecahedron and icosahedron (although I use the word "solids", we are only interested in their surfaces; "regular" here means that all the polygons used are identical and equilateral, and the same number meet at each vertex);
(ii) irregular triangulations of a sphere, for example, mixtures of triangles and pentagons;
(iii) a triangulation of a doughnut;
(iv) a triangulation of a doughnut with two holes.