 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Published 1997 Revised 2012
The Cyclic Quadrilateral
Cyclic quadrilaterals are quadrilaterals with all four of their vertices on a circle.
You can have cyclic polygons of any number of sides.
Not all quadrilaterals are cyclic. Perhaps you can draw a quadrilateral that is not cyclic - how do you know it is not cyclic?
All triangles are cyclic - how could you prove this?
Cyclic quadrilaterals have some interesting features and in this brief article we invite you to look at some of them and we suggest ideas for looking further:
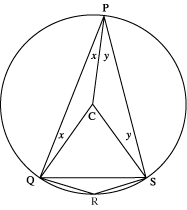
Consider any cyclic quadrilateral $P Q R S$ with vertices on a circle centre $C$.
Draw chord $Q S$ and radii $P C$, $Q C$ and $S C$.
Let angle $Q P C=x$ degrees and angle $S P C=y$ degrees.
This means that angle $Q P S=(x+y)$ degrees.
The angles of the isosceles triangle $P Q C$ are $x$ degrees, $x$ degrees and $(180-2x)$ degrees.
The angles of the isosceles triangle $P S C$ are $y$ degrees, $y$ degrees and $(180-2y)$ degrees.
Angle $Q C S=360$ degrees $-$ angle $Q C P -$ angle $S C P=(2x+2y)$ degrees.
This shows that angle $Q C S$ is twice angle $Q P S$.
We say that angle $Q P S$ is subtended by the arc $Q R S$ and this basic property leads to the following theorems.
You might like to use the Geoboard environment to help investigate these ideas practically before moving into the theory.
Theorem 1.
The angle at the centre of a circle is twice the angle at the circumference subtended by the same arc.
Because angle $Q C S$ is the same for all positions of $P$, Theorem 1 shows angle $Q P S$ is the same regardless of where $P$ lies.
See this problem for a practical demonstration of this theorem.
Theorem 2.
All angles in the same segment of a circle are equal (that is angles at the circumference subtended by the same arc).
Theorem 3.
The angle subtended by a semicircle (that is the angle standing on a diameter) is a right angle. See this problem for a practical demonstration of this theorem.
Theorem 4.
Opposite angles of a cyclic quadrilateral add up to 180 degrees. See this problem for a practical demonstration of this theorem.