 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Published 1997 Revised 2011
Pythagorean Triples I
This is the first of two articles on right-angled triangles whose sides have lengths that are whole numbers. The second article is called "Pythagorean Triples II". Both of these articles can be read in conjunction with the article "Picturing Pythagorean Triples".
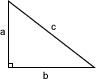
The whole numbers a, b, c are a Pythagorean triple if a and b are the lengths of the two sides of a right-angled triangle with hypotenuse c, so by Pythagoras' Theorem, a ² +b ² =c ² .
In this article we shall look at a way of finding many Pythagorean triples, and we shall also see that whatever whole number n> 3 you choose, there is always a right-angled triangle with one side of length n.
Notice that there may be two (or more) right-angled triangles with the same hypotenuse ; for example:
(there are many examples of this type, but they are not easy to find).
If we are given a right-angled triangle we can always apply an enlargement to it (for example, we can double all lengths) and get another right-angled triangle. This means that from a given triple a,b,c we can produce many more Pythagorean triples na,nb,nc for any whole number n.
For example, starting with the triple 3,4,5 and taking n=5 we get the new triple 15,20,25. Sometimes we can reverse this process by starting with a triple and then reducing the lengths of the sides to get another triple.
This does not always work ; if we start with 3,4,5, for example, and halve the lengths of the sides we do not get a triple of whole numbers. However, sometimes we do ; for example, by halving lengths the triple 10,24,26 converts into the triple 5,12,13.
The most famous Pythagorean triple of all is 3,4,5, and another is 5,12,13. In these two examples, c=b+1, and there are many more examples of this type. Take any number k, and put:
then we always have a ² +b ² =c ²
(an algebraic proof of this is given at the end of this article).
For example, k=1 gives the triple 3,4,5 and k = 2 gives 5,12,13. Try this with other values of k and check that you always get a Pythagorean triple. Clearly, by taking different values of k this method will produce as many Pythagorean triples as we want.
In fact, given any odd number we can always produce a right-angled triangle with one side of this length ; for example, if the odd number is 17, we take k=8 so that a=17, b = 144 and c= 145.
There is another similar way to produce many Pythagorean triples ; this time we take any whole number m and write
Again, we always have a ² +b ² =c ²
(and again, an algebraic proof of this is given at the end of this article).
For example, if we take m=4 we get a=8, b=15 and c=17.
Notice that in this case, if we are given an even number, we can always produce a right-angled triangle with one side of this length ; for example, if the even number is 18, we take m=9 so that a=18, b=80 and c= 82.
In the methods (2) and (3) for constructing triples a,b,c, the difference between the hypothenuse and the longest side is either 1 or 2. There are many triples in which this is not so, and we now give a third method for constructing triples. This method is important because when combined with enlargements to get smaller or larger triangles, this method produces all Pythagorean triples.
We will prove this fact in the second of these two articles.
The third method of producing Pythagorean triples is to take any whole numbers p and q with p> q and write
a = 2pq, b =p ² -q ² , c = p ² +q ² , (4)
Again, we always have a ² +b ² =c ² .
For example, if we take p=4 and q=3 we get a=24, b=7 and c=25. What do we get if we take p=4 and q=1, or if we take p=5 and q=2?
It is worth noting that this last method includes both of the previous ones, for if we take p=k+1 and q=k in (4), we get (2) (with a and b interchanged), and if we take p=m and q=1 in (4), we get (3).
The values p=5 and q=2 give the Pythagorean triple a=20, b = 21 and c=29 and this triple does not arise out of (2) or (3) for any choice of k or m. This shows that (4) is much better than even (2) and (3) combined.
There are some games here that you can play with a friend. First, you must both agree on whether you are to use (2), (3) or (4) ;
let us suppose you choose to use (4). You then choose p and q, and calculate a,b,c from (4). Next, you give these values (but not the values of p and q) to your friend who then has to find the values of p and q that you started with. Playing this game will help you to understand this article.
If you are interested in computing, you might like to try to persuade your computer to find Pythagorean triples for you. For example, the following programme (written in BASIC) will produce a lot of triples, and also give many examples as in (1).
10 FOR C = 1 TO 100
20 FOR B = 1 TO C
30 FOR A = 1 TO B
40 IF A^2+B^2=C^2 PRINT A,B,C
56 NEXT A
60 NEXT B
70 NEXT C
80 STOP
Finally, as promised, we show that a ² +b ² =c ² in each of the cases (2), (3) and (4). In (2) we have a=2k+1, b = 2k ² +2k and c=b+1 so that in this case
c ² -b ² = (c-b)(c+b) = c+b = 2b+1 = 4k ² +4k+1 = (2k+1) ² = a ² .
In (3) we have a = 2m, b =m ² -1 and c = m ² +1 so that in this case
c ² -b ² = (c-b)(c+b) = 2(2m ² ) = (2m) ² = a ² .
Finally, in (4) we have a = 2pq, b =p ² -q ² and c = p ² + q ² so that in this case
c ² -b ² = (c-b)(c+b) = (2q ² ) (2p ² ) = (2pq) ² = a ².
See "Pythagorean Triples II" for the second part of the series.