Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Fraction Lengths
Age 7 to 11
Challenge Level 





Here are some lengths, which could be made out of connecting cubes or strips of coloured paper/card:
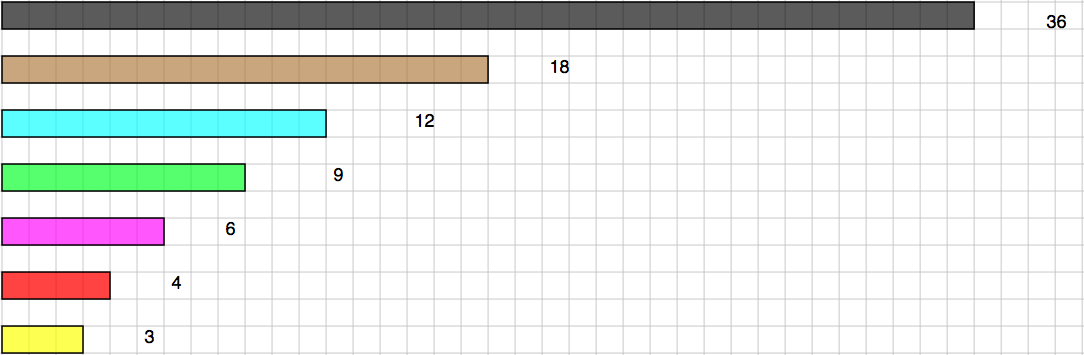
To start with, the black will be counted as ONE so that the brown one is $\frac{1}{2}$, the blue one is $\frac{1}{3}$, etc.
Using different combinations, put them together to equal the length of the black, which is 36 long.
For example, if you were to choose the brown, blue and magenta (pink) you could write them down as the $\frac{1}{2}$, $\frac{1}{3}$, $\frac{1}{6}$
So we would have: $\frac{1}{2} + \frac{1}{3} + \frac{1}{6} = 1$
- - - - - - - - - - - - - - - - - -
MOVING ON
Choose any four of the strips, except the black one, and put them together.Now, compare them with the black.
Here are two examples to start you off. Have a go and find as many different fours as you can.

Using a 3, 6, 12 and an 18 makes 1$\frac{1}{12}$

Using two 12s and two 9s makes 1$\frac{1}{6}$
- - - - - - - - - - - - - - - - - -
GOING EVEN FURTHER
Now the light blue strip is the ONE (1). Use the same fours that you chose before but this time, compare them with the light blue strip instead of the black.
Here are the examples used above, but this time compared with a light blue:

Comparing these four to the light blue it makes 3$\frac{1}{4}$

Comparing these four to the light blue it makes 3$\frac{1}{2}$
Now you go ahead with the fours that you have chosen.
- - - - - - - - - - - - - - - - - -
What can you say about the results you got when comparing your fours with black and comparing them with the light blue?